Homework Help is Here – Start Your Trial Now!
Math
Advanced Math
- kel - ere k > 0 andcz 0. In Section 3.1 we saw that in the case c=o the linear differential equation dP/dt = kP is a mathematical model of a population P(t) that exhibits unbounded growth over the infinite time interval [0, c0), that is. )- co as t- 0o. See Example 1 in that section. (a) Suppose for c 0.01 that the nonlinear differential equation = kp1.01 k > 0, is a mathematical model for a population of small animals, where time t is measured in months. Solve the differential equation subject to the initial condition P(0) = 10 and the fact that the animal population has doubled in 8 months. (Round the coefficient of t to six decimal places.) P(t) = (b) The differential equation in part (a) is called a doomsday equation because the population P(t) exhibits unbounded growth over a finite time interval (0, T), that is, there is some time T such that P(t) - co as t-T. Find (Round your answer to the nearest month.) T= months (c) From part (a), what is P(70)? P(140)? (Round your answers to the nearest whole number.) P(70) = P(140) =

- kel - ere k > 0 andcz 0. In Section 3.1 we saw that in the case c=o the linear differential equation dP/dt = kP is a mathematical model of a population P(t) that exhibits unbounded growth over the infinite time interval [0, c0), that is. )- co as t- 0o. See Example 1 in that section. (a) Suppose for c 0.01 that the nonlinear differential equation = kp1.01 k > 0, is a mathematical model for a population of small animals, where time t is measured in months. Solve the differential equation subject to the initial condition P(0) = 10 and the fact that the animal population has doubled in 8 months. (Round the coefficient of t to six decimal places.) P(t) = (b) The differential equation in part (a) is called a doomsday equation because the population P(t) exhibits unbounded growth over a finite time interval (0, T), that is, there is some time T such that P(t) - co as t-T. Find (Round your answer to the nearest month.) T= months (c) From part (a), what is P(70)? P(140)? (Round your answers to the nearest whole number.) P(70) = P(140) =

Advanced Engineering Mathematics
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
See similar textbooks
icon
Related questions
Question
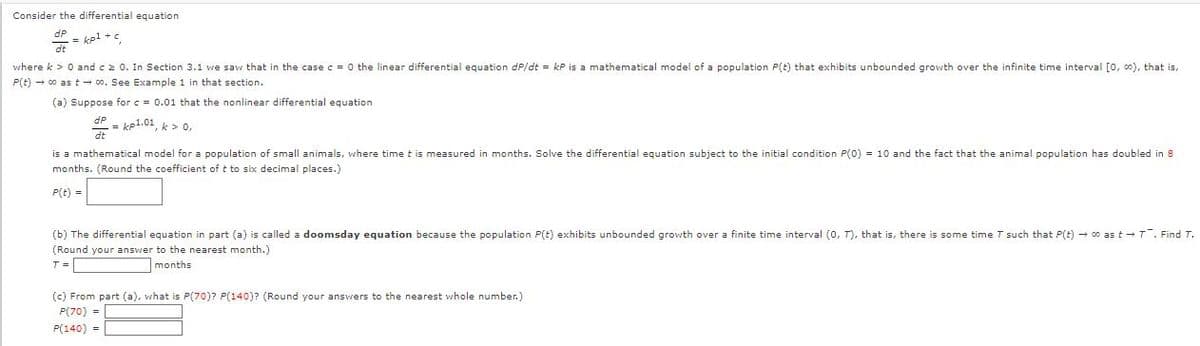
Consider the differential equation dP - = kpl +c dt where k > 0 and c 2 0. In Section 3.1 we saw that in the case c = 0 the linear differential equation dP/dt = kP is a mathematical model of a population P(t) that exhibits unbounded growth over the infinite time interval [0, co0), that is, P(t) - c0 as t - co. See Example 1 in that section. (a) Suppose for c = 0.01 that the nonlinear differential equation = kp1.01, k > o, is a mathematical model for a population of small animals, where time t is measured in months. Solve the differential equation subject to the initial condition P(0) = 10 and the fact that the animal population has doubled in 8 months. (Round the coefficient of t to six decimal places.) P(t) = (b) The differential equation in part (a) is called a doomsday equation because the population P(t) exhibits unbounded growth over a finite time interval (0, T), that is, there is some time T such that P(t) – co ast-T. Find T. (Round your answer to the nearest month.) T = months (c) From part (a), what is P(70)? P(140)? (Round your answers to the nearest whole number.) P(70) = P(140) =
Transcribed Image Text:Consider the differential equation dP - = kpl +c dt where k > 0 and c 2 0. In Section 3.1 we saw that in the case c = 0 the linear differential equation dP/dt = kP is a mathematical model of a population P(t) that exhibits unbounded growth over the infinite time interval [0, co0), that is, P(t) - c0 as t - co. See Example 1 in that section. (a) Suppose for c = 0.01 that the nonlinear differential equation = kp1.01, k > o, is a mathematical model for a population of small animals, where time t is measured in months. Solve the differential equation subject to the initial condition P(0) = 10 and the fact that the animal population has doubled in 8 months. (Round the coefficient of t to six decimal places.) P(t) = (b) The differential equation in part (a) is called a doomsday equation because the population P(t) exhibits unbounded growth over a finite time interval (0, T), that is, there is some time T such that P(t) – co ast-T. Find T. (Round your answer to the nearest month.) T = months (c) From part (a), what is P(70)? P(140)? (Round your answers to the nearest whole number.) P(70) = P(140) =
Expert Solution
trending now

Trending now

This is a popular solution!

steps

Step by step

Solved in 4 steps

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Recommended textbooks for you
Advanced Engineering Mathematics
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Mathematics For Machine Technology
Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,
Basic Technical Mathematics
Basic Technical Mathematics
Advanced Math
ISBN:
9780134437705
Author:
Washington
Publisher:
PEARSON
Topology
Topology
Advanced Math
ISBN:
9780134689517
Author:
Munkres, James R.
Publisher:
Pearson,
SEE MORE TEXTBOOKS