Ionic Equilibrium
Chemical equilibrium and ionic equilibrium are two major concepts in chemistry. Ionic equilibrium deals with the equilibrium involved in an ionization process while chemical equilibrium deals with the equilibrium during a chemical change. Ionic equilibrium is established between the ions and unionized species in a system. Understanding the concept of ionic equilibrium is very important to answer the questions related to certain chemical reactions in chemistry.
Arrhenius Acid
Arrhenius acid act as a good electrolyte as it dissociates to its respective ions in the aqueous solutions. Keeping it similar to the general acid properties, Arrhenius acid also neutralizes bases and turns litmus paper into red.
Bronsted Lowry Base In Inorganic Chemistry
Bronsted-Lowry base in inorganic chemistry is any chemical substance that can accept a proton from the other chemical substance it is reacting with.
Identify the correct conjugate acid-base pair given the following reaction:
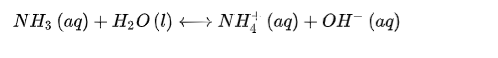
Step by step
Solved in 2 steps with 2 images







