Part D Constants A 400.0-m-wide river flows from west to east at 30.0 m/min. Your boat moves at 100.0 m/min relative to the water no matter which direction you point it. To cross this river, you start from a dock at point A on the south bank. There is a boat landing directly opposite at point B on the north bank, and also one at point C, 75.0 m downstream from B (the figure (Figure 1)) To reach point C at what bearing (angle north of west) must you aim your boat? "Bearing" means the direction of the boat with respect to the water, not the land. Again, you should imagine that you can only look at the water to determine your direction (and not use a compass, or look at features on shore to make corrections in the direction) and that this direction is maintained for the entire trip across the river. Hint: the main point of this part of the problem is to encourage you to use the Galilean velocity vector formula. Let G be the frame attached to the ground, and Frame R be floating with the river. The object of interest that is moving is the boat - label it b. The velocity formula becomes VbG VbR+VRG. The issue here is that you only know the magnitude of the vector VbR (not the direction), and the direction of VbG but not the magnitude. The direction of VbG is given by the direction of vector that points from point A to point C. But, you have all the vector information for the direction of the water in the river, VRG. For these types of vector problems, you want to invoke the law of sines or the law of cosines because the 3 vectors in the Galilean velocity formula form a triangle. In this problem you have the lengths of two of the sides of the triangle and one angle. This is sufficient to get all the sides and all the angles using the law of sines and/or law of cosines north of west Submit Request Answen Part E Refer to part D. How long (t) will it take to cross the river? Hint: Once you have the velocity vector, VbG (both the magnitude and direction) from the previous part D, find the component "y" component (or the North-South component). The time is just the width of the river divided by the y component of velocity min Submit Request Answen Figure 1 of 1 Part F Refer to part D. What distance (d, as measured by an observer on the ground) do you travel? 400.0 m 30.0 mmin Submit Request Answen
Part D Constants A 400.0-m-wide river flows from west to east at 30.0 m/min. Your boat moves at 100.0 m/min relative to the water no matter which direction you point it. To cross this river, you start from a dock at point A on the south bank. There is a boat landing directly opposite at point B on the north bank, and also one at point C, 75.0 m downstream from B (the figure (Figure 1)) To reach point C at what bearing (angle north of west) must you aim your boat? "Bearing" means the direction of the boat with respect to the water, not the land. Again, you should imagine that you can only look at the water to determine your direction (and not use a compass, or look at features on shore to make corrections in the direction) and that this direction is maintained for the entire trip across the river. Hint: the main point of this part of the problem is to encourage you to use the Galilean velocity vector formula. Let G be the frame attached to the ground, and Frame R be floating with the river. The object of interest that is moving is the boat - label it b. The velocity formula becomes VbG VbR+VRG. The issue here is that you only know the magnitude of the vector VbR (not the direction), and the direction of VbG but not the magnitude. The direction of VbG is given by the direction of vector that points from point A to point C. But, you have all the vector information for the direction of the water in the river, VRG. For these types of vector problems, you want to invoke the law of sines or the law of cosines because the 3 vectors in the Galilean velocity formula form a triangle. In this problem you have the lengths of two of the sides of the triangle and one angle. This is sufficient to get all the sides and all the angles using the law of sines and/or law of cosines north of west Submit Request Answen Part E Refer to part D. How long (t) will it take to cross the river? Hint: Once you have the velocity vector, VbG (both the magnitude and direction) from the previous part D, find the component "y" component (or the North-South component). The time is just the width of the river divided by the y component of velocity min Submit Request Answen Figure 1 of 1 Part F Refer to part D. What distance (d, as measured by an observer on the ground) do you travel? 400.0 m 30.0 mmin Submit Request Answen
University Physics Volume 1
18th Edition
ISBN:9781938168277
Author:William Moebs, Samuel J. Ling, Jeff Sanny
Publisher:William Moebs, Samuel J. Ling, Jeff Sanny
Chapter2: Vectors
Section: Chapter Questions
Problem 2.1CYU: Check Your Understanding Two motorboats named Alice and Bob are moving on a lake. Given the...
Related questions
Question
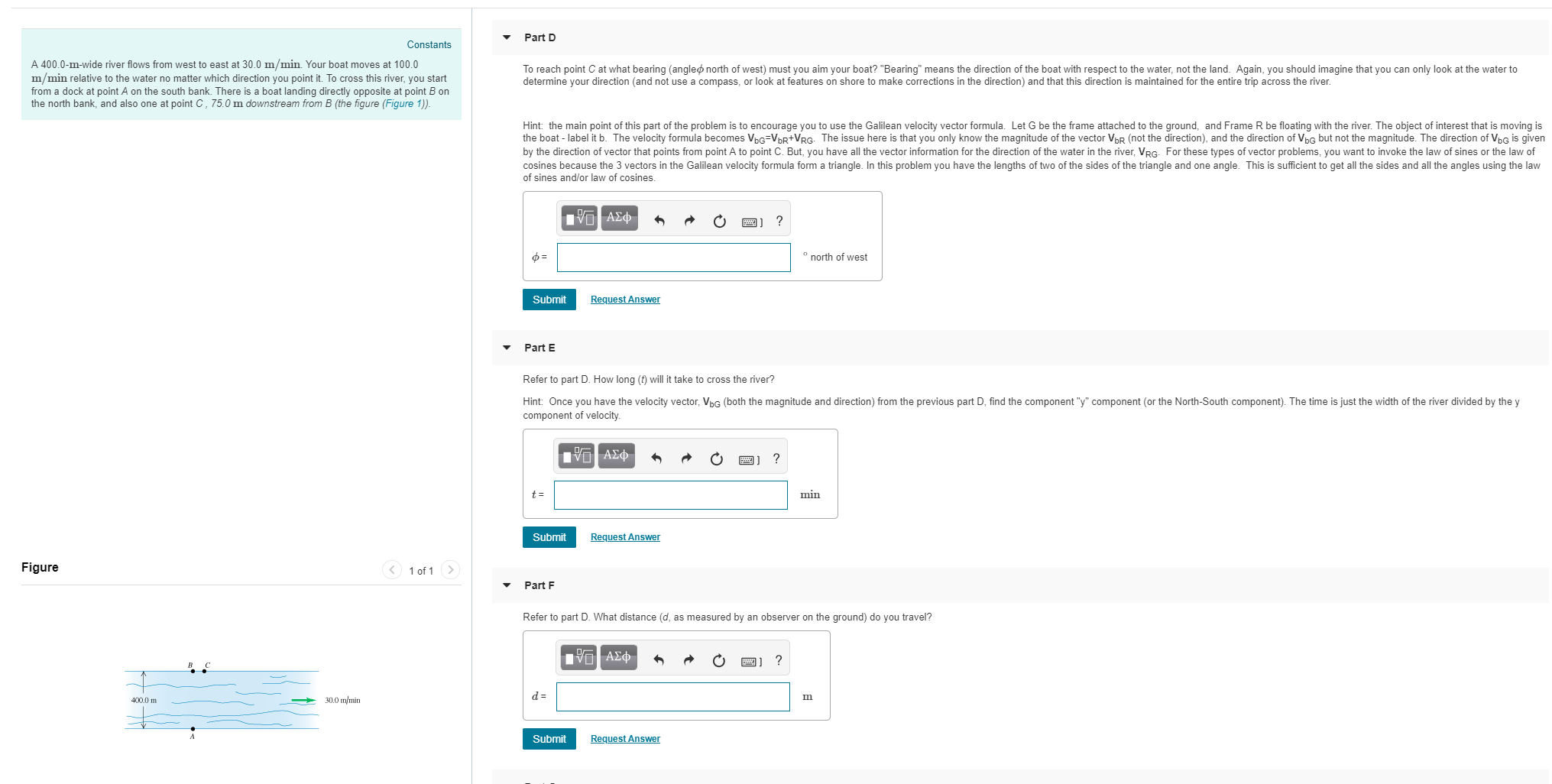
Transcribed Image Text:Part D
Constants
A 400.0-m-wide river flows from west to east at 30.0 m/min. Your boat moves at 100.0
m/min relative to the water no matter which direction you point it. To cross this river, you start
from a dock at point A on the south bank. There is a boat landing directly opposite at point B on
the north bank, and also one at point C, 75.0 m downstream from B (the figure (Figure 1))
To reach point C at what bearing (angle north of west) must you aim your boat? "Bearing" means the direction of the boat with respect to the water, not the land. Again, you should imagine that you can only look at the water to
determine your direction (and not use a compass, or look at features on shore to make corrections in the direction) and that this direction is maintained for the entire trip across the river.
Hint: the main point of this part of the problem is to encourage you to use the Galilean velocity vector formula. Let G be the frame attached to the ground, and Frame R be floating with the river. The object of interest that is moving is
the boat - label it b. The velocity formula becomes VbG VbR+VRG. The issue here is that you only know the magnitude of the vector VbR (not the direction), and the direction of VbG but not the magnitude. The direction of VbG is given
by the direction of vector that points from point A to point C. But, you have all the vector information for the direction of the water in the river, VRG. For these types of vector problems, you want to invoke the law of sines or the law of
cosines because the 3 vectors in the Galilean velocity formula form a triangle. In this problem you have the lengths of two of the sides of the triangle and one angle. This is sufficient to get all the sides and all the angles using the law
of sines and/or law of cosines
north of west
Submit
Request Answen
Part E
Refer to part D. How long (t) will it take to cross the river?
Hint: Once you have the velocity vector, VbG (both the magnitude and direction) from the previous part D, find the component "y" component (or the North-South component). The time is just the width of the river divided by the y
component of velocity
min
Submit
Request Answen
Figure
1 of 1
Part F
Refer to part D. What distance (d, as measured by an observer on the ground) do you travel?
400.0 m
30.0 mmin
Submit
Request Answen
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 8 steps with 7 images

Recommended textbooks for you

University Physics Volume 1
Physics
ISBN:
9781938168277
Author:
William Moebs, Samuel J. Ling, Jeff Sanny
Publisher:
OpenStax - Rice University

Principles of Physics: A Calculus-Based Text
Physics
ISBN:
9781133104261
Author:
Raymond A. Serway, John W. Jewett
Publisher:
Cengage Learning

University Physics Volume 1
Physics
ISBN:
9781938168277
Author:
William Moebs, Samuel J. Ling, Jeff Sanny
Publisher:
OpenStax - Rice University

Principles of Physics: A Calculus-Based Text
Physics
ISBN:
9781133104261
Author:
Raymond A. Serway, John W. Jewett
Publisher:
Cengage Learning