Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Related questions
Question
Show that you have reasoned about the problem a way that is correct
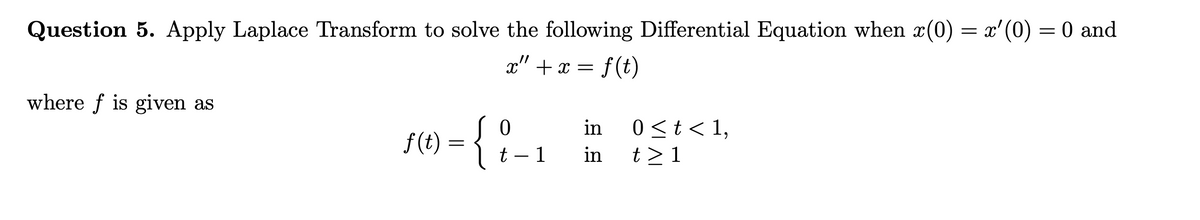
Transcribed Image Text:Question 5. Apply Laplace Transform to solve the following Differential Equation when x(0) = x'(0) = 0 and
x" + x = f(t)
where f is given as
f(t)
=
{}
t-1
in 0 < t < 1,
in
t>1
![(a) i = √-1 and eit = cost + i sin t.
(b) For all integer n ≥ 0 we have:
cos(nx) = (−1)ª, sin(nx) = 0, sin ((2n + 1)2) = (−1)”, cos ((2n
(2n +1)
- 1977)
= 0.
(c) Integration by Parts: fudv=uv - fvdu.
(d) Quadratic formula: If ar² + br+c=0 for a 0. Then,
(e) Laplace Transform: F(s) = f est f(t)dt.
(f) Convolution: (f* g)(t) = fő ƒ (0)g(t — 0)d0. Note (ƒ * g)(t) = (g * f)(t).
(g) LT of f(t) = sin at, f(t) = cos at and f(t) = t" for n ≥ 0:
S
L[sin at]
and L[cos at]
s² + a²
(h) Properties of LT/ILT:
u₁ (t) =
a
s² + a²
==
r =
(k) Change of variables:
-b ± √b² - 4ac
2a
(1) LT/ILT are linear operators.
(2) Shift/Scaling: L[eat f(t)] | = F(s − a) for constant a € R and L[f(at)] = F() for constant a > 0.
(3) LT of derivatives: L[f(n) (t)] = sn F (s) — :
· sn-¹ƒ(0) — sn-2 f'(0) - ... - fn-¹(0) for n ≥ 1.
● LT of integrals: L [Ső f(0)d0] = F(s) when f(0) = 0.
(4) Derivative of LT or LT of multiplication by polynomials: L[t" f(t)] = (-1)" de F(s) for n ≥ 1.
(5) Unit Step Function: L[He(t)f(t — c)] = F(s)e-sc.
(6) Convolution Property: L[(f* g)(t)] = F(s)G(s).
(i) Formula for Reduction of Order:
/ [₁
x₂ (t) = x₁(t)
√ [²
(j) Formula for Variation of Parameters: xp(t) = x₁(t)u₁(t) + x₂(t)u₂(t) when
x₂(t)g(t)
dt
= /[ W
e-Sp(t)dt
x²(t)
and L[t”] :
and u₂(t) =
• Euler equation s = lnt or t = e³,
• Bernoulli equation: z = x-k,
• k-homogeneous equation: zor x = zt.
dt
n!
gn+1
x₁
W(x1, x2)(t)
dt](https://content.bartleby.com/qna-images/question/d76a2d57-02e6-4734-ba8a-6fadc8c476a5/6bcedb34-87de-45b0-bdbf-67a11bd5bf79/trp0b52_processed.png)
Transcribed Image Text:(a) i = √-1 and eit = cost + i sin t.
(b) For all integer n ≥ 0 we have:
cos(nx) = (−1)ª, sin(nx) = 0, sin ((2n + 1)2) = (−1)”, cos ((2n
(2n +1)
- 1977)
= 0.
(c) Integration by Parts: fudv=uv - fvdu.
(d) Quadratic formula: If ar² + br+c=0 for a 0. Then,
(e) Laplace Transform: F(s) = f est f(t)dt.
(f) Convolution: (f* g)(t) = fő ƒ (0)g(t — 0)d0. Note (ƒ * g)(t) = (g * f)(t).
(g) LT of f(t) = sin at, f(t) = cos at and f(t) = t" for n ≥ 0:
S
L[sin at]
and L[cos at]
s² + a²
(h) Properties of LT/ILT:
u₁ (t) =
a
s² + a²
==
r =
(k) Change of variables:
-b ± √b² - 4ac
2a
(1) LT/ILT are linear operators.
(2) Shift/Scaling: L[eat f(t)] | = F(s − a) for constant a € R and L[f(at)] = F() for constant a > 0.
(3) LT of derivatives: L[f(n) (t)] = sn F (s) — :
· sn-¹ƒ(0) — sn-2 f'(0) - ... - fn-¹(0) for n ≥ 1.
● LT of integrals: L [Ső f(0)d0] = F(s) when f(0) = 0.
(4) Derivative of LT or LT of multiplication by polynomials: L[t" f(t)] = (-1)" de F(s) for n ≥ 1.
(5) Unit Step Function: L[He(t)f(t — c)] = F(s)e-sc.
(6) Convolution Property: L[(f* g)(t)] = F(s)G(s).
(i) Formula for Reduction of Order:
/ [₁
x₂ (t) = x₁(t)
√ [²
(j) Formula for Variation of Parameters: xp(t) = x₁(t)u₁(t) + x₂(t)u₂(t) when
x₂(t)g(t)
dt
= /[ W
e-Sp(t)dt
x²(t)
and L[t”] :
and u₂(t) =
• Euler equation s = lnt or t = e³,
• Bernoulli equation: z = x-k,
• k-homogeneous equation: zor x = zt.
dt
n!
gn+1
x₁
W(x1, x2)(t)
dt
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 2 images
Knowledge Booster
Similar questions
- Hello, Can you explain problem c) I do not understand the solution.arrow_forwardThe following system has an infinite number of solutions. Form an augmented matrix, then write the matrix in the reduced form. Write the reduced form of the matrix below and then write the solution in terms of z. The required augmented matrix is: 4x 8x 12x + a11 C a21 a31 2y + 1z = 4 4y + 2z 1 2y + 3z = 5 a 12 a22 a32 a13 a23 a33 b₁ b2 = ხვა 2arrow_forwardI am lost on what to do. I've tried to list what I know, but I got confused and have no leads. I'm working on Problem 3. Pleases help and show steps how to work out problem.arrow_forward
- Hey there, Here is a proof I have been struggling to solve can someone help?arrow_forwardP = 0 1 1 0 and D = 6 0 0 11 do not seem to be the correct answers, may there be a mistake somewhere? I went through by myself and got a similar answer, but it was also deemed incorrect. Just a bit confused.arrow_forwardThis doesn't make sense, a and b are already defined in the problem as 1...arrow_forward
- In each case below, in what ways are the figures alike? (Select all that apply.) (a) (b) оооооо оооооо (i) Shape (iii) would be similar to shape (ii) if two sides were removed and one was added. Shapes (i) and (iii) both have 4 sides. Shapes (i) and (ii) are both convex. Shapes (ii) and (iii) are both convex. Shape (iii) would be similar to shape (i) if two sides were removed and one was added. Shapes (ii) and (iii) both have 3 sides. e (ii) All three shapes are convex. Shapes (ii) and (iii) have the same number of sides. Shape (ii) would be similar to shape (i) if two sides were removed and one was added. Shapes (i) and (iii) have the same number of sides. Shape (iii) would be similar to shape (i) if two sides were removed and one was added. All three shapes are concave.arrow_forwardPlease show as much work as possible, and please do not skip steps. I really want to learn how to solve this, so if you use a axiom please include it. Problem Statement: One out of every one- thousand people have disease X. A new test for X is available, but it's not very accurate. If you have X, there is an 80% chance the test comes back positive and a 20% chance it comes back negative. If you don't have X, there is a 60% chance the test comes back negative and a 40% chance it comes back positive. Question: You are randomly chosen to be tested for X. Since the test is not very accurate, you areadministered the test 10 times; assume the outcomes of these 10 tests are independent. Sevenout of the 10 tests come back positive. Given these test results, what is the probability youhave X?arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
- Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY 
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,