= xtraor- ld be engendered by imaginary numbers. From this time of their mystical character, although their full acceptance the roots of the cubic x in the 1800s. 1 36r2= 20x + 56. (c) 3 (d) x64 6x2+ 24x. 2. Derive Cardan's formula p'3 + 27 q2 V 4 3q 3q V 4 2 2 27 for solving the cubic equation x3 p>O and q> 0. = px +q, where 12 3. Using Cardan's formula, obtain one root of each of the ++ Cardan's Ars Magna following cubic equations. HIB (a) x3+24x 16. (b) x315x6x218 (c) x327 (d) x39x 12. 6x2+15x +8 3x2+27x+ 41. AN 6x2+58. . AR (e) x3 = (f) x3= 4. Solve the cubic equation x+6x2+x =14. Problems 5-11 appear in Cardan's Ars Magna. 5. Chapter 5, Problem 2. There were two leaders, each whom divided 48 aurei among his soldiers. One of these had two more soldiers than the other. The one who had two soldiers fewer had four aurei more for each soldier. Find how many soldiers each had. 6.Chapter 37, Problem 1. The dowry of Francis's wife 100 more than Francis's own property is worth quare of the dou aurei and the than the 100 nore SS
Percentage
A percentage is a number indicated as a fraction of 100. It is a dimensionless number often expressed using the symbol %.
Algebraic Expressions
In mathematics, an algebraic expression consists of constant(s), variable(s), and mathematical operators. It is made up of terms.
Numbers
Numbers are some measures used for counting. They can be compared one with another to know its position in the number line and determine which one is greater or lesser than the other.
Subtraction
Before we begin to understand the subtraction of algebraic expressions, we need to list out a few things that form the basis of algebra.
Addition
Before we begin to understand the addition of algebraic expressions, we need to list out a few things that form the basis of algebra.
#3 a and b

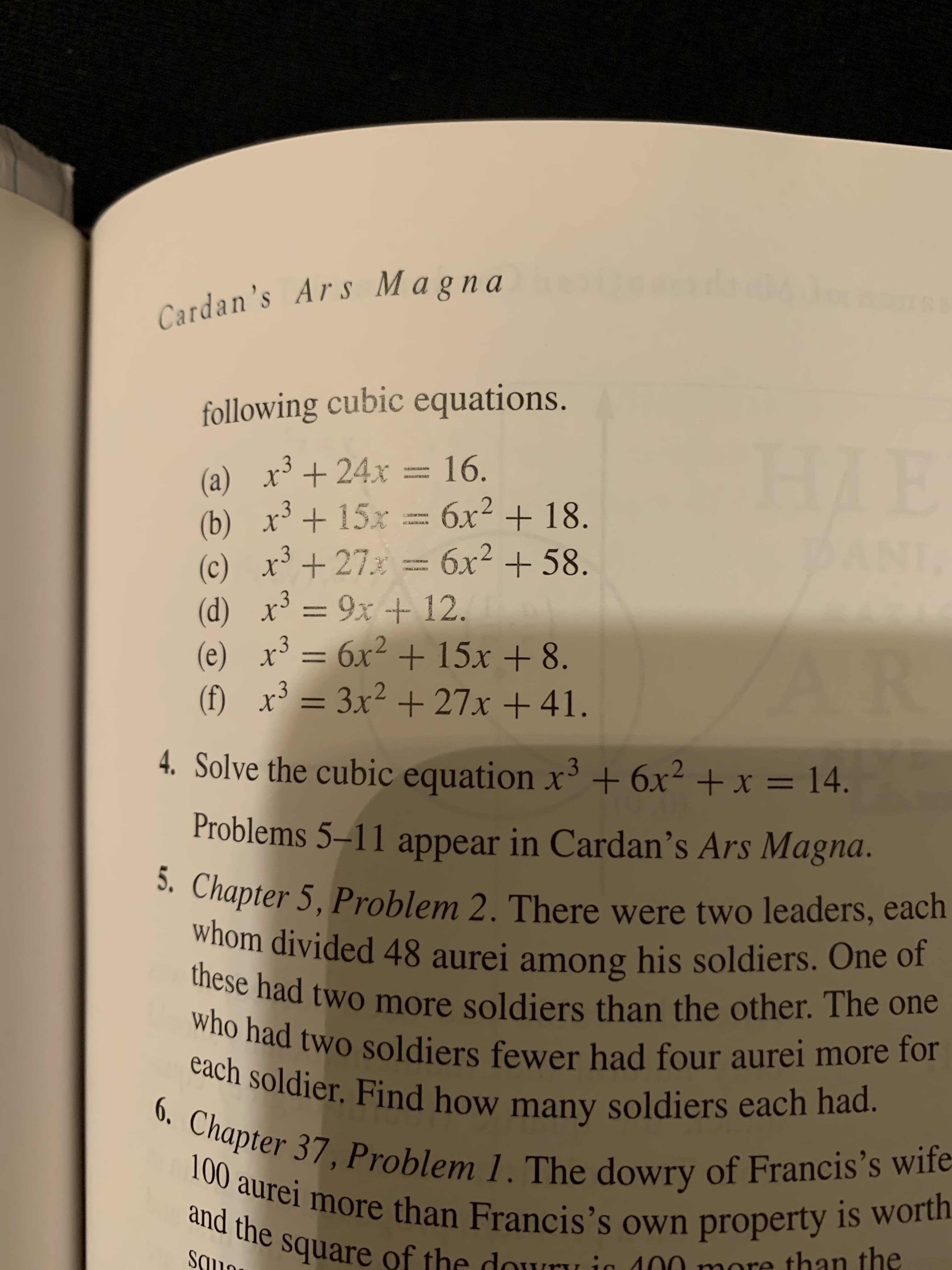
Trending now
This is a popular solution!
Step by step
Solved in 8 steps with 15 images









