What are Numbers?
Numbers are some measures used for counting. They can be compared one with another to know its position in the number line and determine which one is greater or lesser than the other.
Suppose that your friend gives you a pack of pencils and ask you to open and tell how many pencils are there. You have to tell by counting the pencils. But what will you tell after counting? You have to tell a representation which will exactly tell how much you have counted by a symbol. This is where numbers are used. If you count 5 objects, then 5 is the number used for representing the total objects you have counted.
What if you did not find any pencil inside? How will you represent it as a number? 0 means that there are no pencils inside. Imagine you are going to shop to buy 1kg sugar. You have 10 rupees in hand. But the actual cost of 1 kg sugar is 15 rupees. Now the shopkeeper asks you to bring 5 rupees later. How much money will you have in balance with you after paying 10 rupees and having a debt of 5 rupees? The answer is not 0 but less than 0. What will this number be defined as?
If there are 4 long pencils and 1 pencil is broken and you find only one part of the broken pencil, think of a way to tell this.
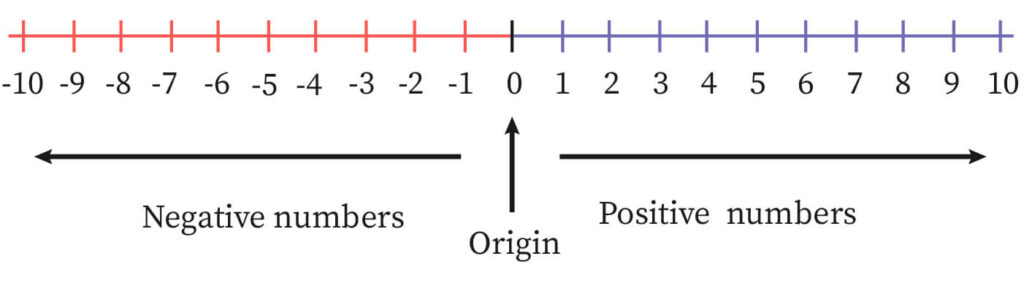
Number Line
It is a line in which numbers are plotted.
Natural Numbers

Natural numbers by definition are the collection of numbers starting from 1,2, 3, and goes till infinity. These are used for counting the objects that can be seen around in everyday life. All the numbers here are positive. So, while adding two positive numbers the result is again a positive number. The leftmost number is the smallest and the value increases moving towards the right. Trying to count the stars in the universe? Is it countable or infinite?
What if 5 is subtracted from 5? Give a thought to this. Will the balance also lie in this collection? No, because this collection does not include 0.
Whole Numbers
Whole numbers are similar to natural numbers except that it includes 0 in the collection. The meaning of the word whole is complete. It starts from 0,1, 2, and goes up to infinity. Suppose you are asked to fill in a form the total amount of money you have in your purse. But you do not have money. Then you will write 0 in the blank. Take two numbers from the collection, let us say, 3 and 5. Subtract 5 from 3. The result will not be in the collection.
Integers
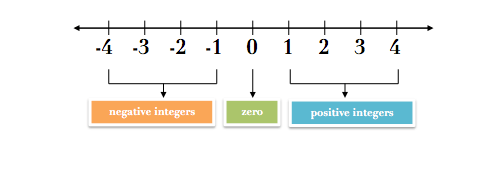
Integers by definition is the collection of positive numbers, zero and negative numbers. They are classified as positive integers, zero and negative integers. Zero is neither positive nor negative. Positive integers include natural numbers 1,2, 3… and negative integers have negative signs before the numbers 1,2,3…. This collection is very big. How to know which one is greater and which is smaller? Here also, the leftmost integer is the smallest and the value increases moving towards the right. But how to know which lies on the left. The number line is used to understand it better.
The numbers left to 0 are negative integers and the numbers right to 0 are positive integers. Moving towards right the value increases and on moving towards the left the value decreases. Now tell if 5 is lesser than 6. Yes, because 5 is to the left of 6. But is -5 lesser than -6? No, because -5 is to the right of -6. -5 is greater than -6.
Suppose that you are watching a film on TV. An actor has one-star shaped biscuit and he wants to share equally with his brother. He must break it into two halves and give one half to his brother. Half is represented as ½. Here the number on the top of the line is called numerator and the number on the bottom of the line is called denominator. Numerator tells the number of biscuits you have, and denominator tells the number of parts you want to break the biscuit. The meaning of ½ is you are going to break 1 into 2 equal parts. But you cannot find an integer with value ½. Here, rational, and irrational numbers come into play.
Rational Numbers
Rational numbers are defined as the numbers in the form of a ratio p/q. The meaning of rational is ratio. The numerator p and the denominator q are integers. Suppose that the time it takes to clean a room is half an hour. Half an hour means half of an hour. 1 hour equals 60 minutes. What is half of it? Divide it by two. It becomes 60/2. In other words, 60 is divided into two parts. This is a rational number because it is of the form p/q where p=60 and q=2 are integers. The quotient is 30. Where is this half in the number line? It is in the middle of 1 and 2.
What about -1/2? Here p=-1 is a negative integer and q=2 is positive. The negative terms lie to the left of 0 in the number line. Now how to locate -1/2 in the number line? It is going to lie in the middle of -1 and -2.
Dividing 1 by 2 the value is 0.5 with 5 in the tenths place occurring after the decimal point. Divide -1/2. The result is -0.5. In both the cases there is only one number after the decimal point.
Try dividing 3 by 4. Is ¾ this a rational number? Yes, because p and q are integers. On dividing 3 by 4 the quotient is 0.75 with 7 in tenths and 5 in hundredths place. After the decimal point there are only 2 numbers. Let us see another case. Divide 1/3 and see how many values there are after the decimal point. The result is 0.33333… and it has unending 3’s after the decimal point. Even though it is unending still it follows the same pattern. This is also a rational number because it follows the same pattern after the decimal point.
Let us see for 1/7. Now divide 1 by 7. The value is 0.142857142857… and has a series of numbers after the decimal point. Still, it follows a pattern 142857 after the decimal point. Therefore 1/7 is a rational number.
So, for a rational number p/q, p and q are integers and dividing p by q follows a repeating pattern or it has a countable number of digits after the decimal point.
Irrational Numbers
Irrational numbers are defined as those which have an endless series of numbers after the decimal point without following any pattern. These numbers cannot be written as a fraction. Example, 1.264378909654229 … is an irrational number because it does not follow a pattern.
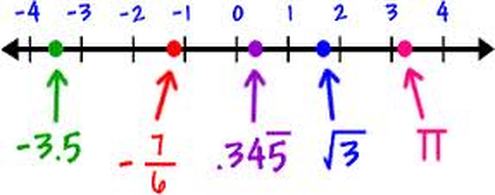
Real Numbers
Real numbers can be defined as the collection of all rational and irrational numbers.
In the above real line, -15/4 and -2.5 are negative integers which are also rational numbers.
Root 2 is irrational, 20/9 is a positive integer and a rational number. The value of π,−π/2 and e are irrational. But all this lies in the real line. This is a bigger collection of numbers.
Context and Applications
This topic is significant in the professional exams for both undergraduate and graduate courses, especially for
- B.Sc. in Mathematics
- M.Sc. in Mathematics
Want more help with your algebra homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Numbers Homework Questions from Fellow Students
Browse our recently answered Numbers homework questions.