Physics for Scientists and Engineers: Foundations and Connections
1st Edition
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Katz, Debora M.
Chapter25: Gauss’s Law
Section25.1: Qualitative Look At Gauss’s Law
Problem 25.1CE: a. List all the uppercase letters that have the same symmetry as A. b. List all the uppercase...
Related questions
Question
A quantity of a monatomic ideal gas undergoes a process in which both its pressure and volume are doubled as shown in Figure P12.18. What is the energy absorbed by heat into the gas during this process? Hint: The internal energy of a monatomic ideal gas at pressure P and occupying volume V is given by U = 3/2PV
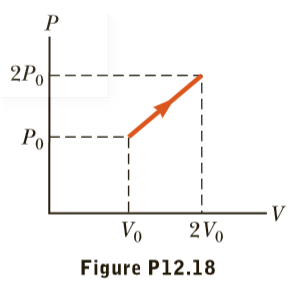
Transcribed Image Text:2Po
Po
2Vo
Vo
Figure P12.18
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 3 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Recommended textbooks for you

Physics for Scientists and Engineers: Foundations…
Physics
ISBN:
9781133939146
Author:
Katz, Debora M.
Publisher:
Cengage Learning

Physics for Scientists and Engineers: Foundations…
Physics
ISBN:
9781133939146
Author:
Katz, Debora M.
Publisher:
Cengage Learning