Chapter7: Electric Potential
Section: Chapter Questions
Problem 32P: (a) What is the average power output of a heart defibrillator that dissipates 400 J of energy in...
Related questions
Question
In the circuit of Figure P18.23, determine (a) the current
in each resistor, (b) the potential difference across the 2.00 x
102 - Ω resistor, and (c) the power delivered by each battery.
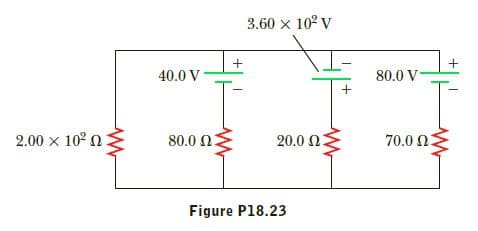
Transcribed Image Text:3.60 x 10° v
80.0 V-
40.0 V
20.0 0.
70.0 2
80.0 Ω
2.00 x 10° n
Figure P18.23
Expert Solution
Trending now
This is a popular solution!
Step by step
Solved in 9 steps with 9 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Recommended textbooks for you

