Related questions
Concept explainers
Recall, from this chapter, that the factor gamma (γ) governs both time dilation and length contraction, where
When you multiply the time in a moving frame by γ, you get the longer (dilated) time in your fixed fame. When you divide the length in a moving frame by γ, you get the shorter (contracted) length in your fixed frame.
According to Newtonian mechanics, the momentum of the bus in the problem 1 is p = mv. According to relativity, it is p = γmv. How does the actual momentum of the bus moving at 0.99c compare with its classical momentum?
problem1
Recall, from this chapter, that the factor gamma (γ) governs both time dilation and length contraction, where
When you multiply the time in a moving frame by γ, you get the longer (dilated) time in your fixed fame. When you divide the length in a moving frame by γ, you get the shorter (contracted) length in your fixed frame.
A passenger on an interplanetary express bus traveling at v = 0.99c takes a 5-minute catnap, according to her watch. Show that her catnap from the vantage point of a fixed planet lasts 35 minutes.
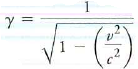
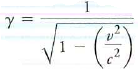
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 3 images
- The time interval ΔΔt between two events measured by an observer moving with respect to a clock1 is usually shorter than the time interval ΔΔtp (ΔΔt < ΔΔtp) between the same two events measured by an observer at rest with respect to the clock. Group of answer choices True Falsearrow_forwardI need help on question 7?arrow_forwardI need help on question 9?arrow_forward
- A particle of mass M, which was initially at rest, is hit by a particle of mass m, which is travelling at the speed Vi. The two particles collide and travel in different directions at the same pace Vf. Find the mass ratio M/m in terms of ß = vi/c, assuming a relativistic, elastic collision. Demonstrate that this reduces to Vi 0, the nonrelativistic meaning.arrow_forwardI am currently working through a physics book (Spacetime Physics by Edwin Taylor) and I have come across this question and I don't know how to solve it: "Take the differential of this equation for g to obtain an approximate algebraic expression for Δg, the change in g, for a small change Δr in height." How do I sovle this question?arrow_forwardCalculate the interval ∆s2 between two events with coordinates ( x1 = 50 m, y1 = 0, z1 = 0,t1 = 1 µs) and (x2 = 120 m, y2 = 0, z2 = 0, t2 = 1.2 µs) in an inertial frame S. b) Now transform the coordinates of the events into the S'frame, which is travelling at 0.6calong the x-axis in a positive direction with respect to the frame S. Hence verify that thespacetime interval is invariant.arrow_forward
- College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON
Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press 
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley
College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON