What is the Special Theory of Relativity?
The theory of special relativity explains the connection between space and time to objects that move in a straight line at a constant speed. The objects move at the speed of light. When an object approaches light speed, its mass is endless and cannot move faster than light. The most crucial postulate of Einstein's special relativity is that the laws of nature do not change in each frame of reference.
Frames of Reference
Einstein's special theory of relativity is based on the idea of reference frames. A reference frame is simply "where a person (or other observers) happens to be standing". You, at this moment, are probably sitting at your computer. That is your current reference frame. You feel like you are stationary, even though you know the earth is revolving on its axis and orbiting around the sun. Here is an important fact about reference frames: There is no such thing as an absolute frame of reference in our universe. By saying absolute, what is meant is that no place in the universe is completely stationary. This statement says that since everything is moving, all motion is relative. Think about it - the earth itself is moving, so even though you are standing still, you are in motion. You are moving through both space and time at all times. Because no place or object in the universe is stationary, there is no single place or object on which to base all other motion. Therefore, if John runs toward Hunter, it could be correctly viewed two ways. From Hunter's perspective, John is moving towards Hunter. From John's perspective, Hunter is moving towards John. Both John and Hunter have the right to observe the action from their respective frames of reference. All motion is relative to your frame of reference. Another example: If you throw a ball, the ball has the right to view itself as being at rest relative to you. The ball can view you as moving away from it, even though you view the ball as moving away from you. Keep in mind that even though you are not moving with respect to the earth's surface, you are moving with the earth.
Time Dilation
In the special theory of relativity, the dilation of time is the change in time or slowing of the time measured by a clock observer in relative motion. A non-accelerating motion observer has a well-defined means of determining which events occur simultaneously as one event in particular relativity. However, a second inertial observer, relative to the first, disagrees with the first observer about what events are simultaneous to that event.
Proper Length
The proper length is defined as the length that is measured in the frame where the object appears to be at rest. While observing an object moving at speed, the relative speed will be the same even though there is a difference in time. So the observers know that the distance depends on the observer's relative motion. The length measurements are quite complex in the theory of relativity. In classical mechanics, a reference to a position of a point is taken to measure the length, but two different observations are made in the theory of relativity. A proper length is the object's length that the observer measures relative to the object, while the length that moves the object to appear to be in motion is the length that is measured in that framework.
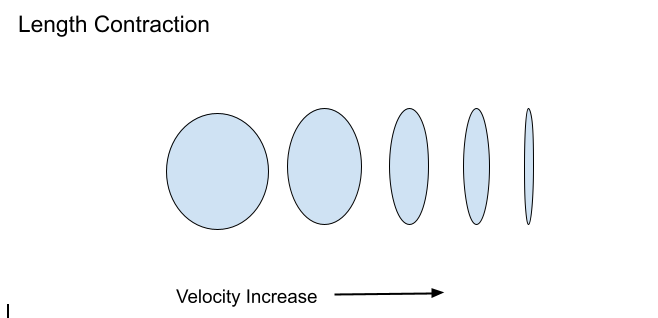
Length Contraction
Length contraction refers to a phenomenon in which an object (which is in motion) is observed to have a diminished length along the dimension of its motion by an observer at rest. It is named after physicists Hendrik Lorentz and George Fitzgerald. The object length contracts, depending upon the speed of the object. More is the speed, more is the contraction. This effect is not observed by humans in daily life but becomes significant only when objects move with an appreciable fraction of the speed of light.
Length contraction L is the diminishing of the measured length of an object which is in motion with respect to the frame of the observer.
Here, L0 is the original length, V is the velocity of the object and C is the speed of light.
Proper Time
In the special theory of relativity, the object travels in three-dimensional spaces of axis x, y, and z. There is another dimension which is the dimension for the time t. The time and length of two different objects in the same frame of reference are relative to their motion, and both the objects have a different value of the proper time. The object travels faster in space and when it is closely related to the speed of the light. For instance, if there two observers in the same frame of reference, where one of them is at rest and the other one is sitting inside a moving object. Like one of the observers can be on Earth, and the other observer is on another planet that is moving faster than the Earth. Let both the observers be twins (of the same age). Now when the observers return from the planet to Earth. The observer on Earth would be aged more than the observer who returned from the other planet. This phenomenon is due to the proper time in the theory of relativity.
The equation of the proper time is :
Here, the phenomenon of time-dilation can be understood. T and T0 are the two kinds of observers.
Here, V is the speed of an object and C is the speed of light.
From the equation, it is understood that the time of inversely proportional to the velocity of the object or body and the speed of light.
Equation of the Proper Length
The length contraction phenomenon is used by Einstein to prove the theory of special relativity mathematically. In the relativity theorem, two observers are standing at different places, where one is sitting stationary on the platform, and the other observer is sitting inside the train. When both of them measures the length of the bench placed on the platform, the length measured by both the observers is different.
The proper length is represented by L0, which is the change in length. The distance is the product of velocity and the change in time.
Let velocity be denoted as v, and the change in time be denoted as ∆t.
Hence the equation is:
If the time relative to the observer on the Earth is ∆t and the object that is moving in space relative to the observer has a time to. Then, the equation of the length contraction or the proper length be:
The length contraction equation with respect to the velocity of the object and the speed of the light moving will be measured as
Here, c is .
NOTE: There is a difference between the proper length and proper distance.
The limitation of the proper length is that the object's acceleration is limited to the values
Here 'a' is the acceleration of the object. For maximum length, there is an infinite acceleration at the rear end of the object and has a limited value at the front end of the acceleration. This becomes a complexity during the experiment of relativity between different objects of different lengths.
Practice Problem:
1)An unstable particle is created in the upper atmosphere from a cosmic ray and travels straight down towards the surface of the Earth with a speed of 0.99650c relative to the Earth. A scientist at rest on the Earth's surface measures that the particle is created at an altitude of 45km.
(a) As measured by the scientist, how much time does it take the particle to travel 45km to the surface of the Earth?
(b) Use the length-contraction formula to calculate the distance from where the particle is created to the surface of the Earth as measured in the particle's frame.
(c) In the particle's frame, how much time does it take for the particle to travel from where it is created to the Earth's surface? Calculate the time of both with the time-dilation formula reference and from a distance calculated in the previous part.
Do the two results agree?
Solution:
a).
b).
c).
Yes, the two results agree.
2) A space ship that has a proper length of 2×102m moves 0.970c relative to the Earth. What is the spaceship's length as measured by an observer on the Earth?
Solution: 48.6 meter
Context and Applications
This topic is significant in the professional exams for both undergraduate and graduate courses, especially for
- Bachelors in Science Physics
- Bachelors in Engineering
Want more help with your physics homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Proper Length Homework Questions from Fellow Students
Browse our recently answered Proper Length homework questions.