(3) Draw the shear force diagram and bending moment diagram of the beam. Indicate the values of shear forces and bending moments at points A, B, C, D and E. (4) Calculate the angle of rotation at point 4. (5) Calculate the vertical deflection at point E. 10 kN/m 2 m BO Im Fig. Q3 2 m DO Im 5 kN
(3) Draw the shear force diagram and bending moment diagram of the beam. Indicate the values of shear forces and bending moments at points A, B, C, D and E. (4) Calculate the angle of rotation at point 4. (5) Calculate the vertical deflection at point E. 10 kN/m 2 m BO Im Fig. Q3 2 m DO Im 5 kN
Mechanics of Materials (MindTap Course List)
9th Edition
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Barry J. Goodno, James M. Gere
Chapter1: Tension, Compression, And Shear
Section: Chapter Questions
Problem 1.3.4P: Segments A B and BCD of beam A BCD are pin connected at x = 4 m. The beam is supported by a sliding...
Related questions
Question

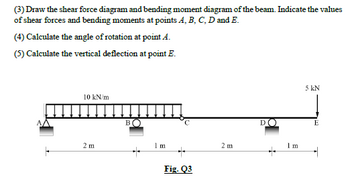
Transcribed Image Text:(3) Draw the shear force diagram and bending moment diagram of the beam. Indicate the values
of shear forces and bending moments at points A, B, C, D and E.
(4) Calculate the angle of rotation at point A.
(5) Calculate the vertical deflection at point E.
þ
10 kN/m
2 m
B
+
1 m
Fig. Q3
2 m
DO
Im
5 kN
E

Transcribed Image Text:Q3 A pin-connected beam as shown in Fig. Q3 is pin-supported at A and roller-supported at B
and D. The beam is subjected to a point load of 5 kN at E and a uniformly distributed loading
of 10 kN/m over region AC. The Young's modulus is 200 GPa, the second moment of area of
beam AC is 100×100 mm, and the second moment of area of beam CE is 200×100 mm*.
(1) Prove that the beam is stable and determinate.
(2) Calculate support reactions at A, B and D of the beam.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 4 steps with 2 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
Question d & e
Transcribed Image Text:(3) Draw the shear force diagram and bending moment diagram of the beam. Indicate the values
of shear forces and bending moments at points A, B, C, D and E.
(4) Calculate the angle of rotation at point A.
(5) Calculate the vertical deflection at point E.
þ
10 kN/m
2 m
B
+
1 m
Fig. Q3
2 m
DO
Im
5 kN
E

Transcribed Image Text:Q3 A pin-connected beam as shown in Fig. Q3 is pin-supported at A and roller-supported at B
and D. The beam is subjected to a point load of 5 kN at E and a uniformly distributed loading
of 10 kN/m over region AC. The Young's modulus is 200 GPa, the second moment of area of
beam AC is 100×100 mm, and the second moment of area of beam CE is 200×100 mm*.
(1) Prove that the beam is stable and determinate.
(2) Calculate support reactions at A, B and D of the beam.
Solution
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Recommended textbooks for you

Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:
9781337093347
Author:
Barry J. Goodno, James M. Gere
Publisher:
Cengage Learning

Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:
9781337093347
Author:
Barry J. Goodno, James M. Gere
Publisher:
Cengage Learning