What is meant by combined loading?
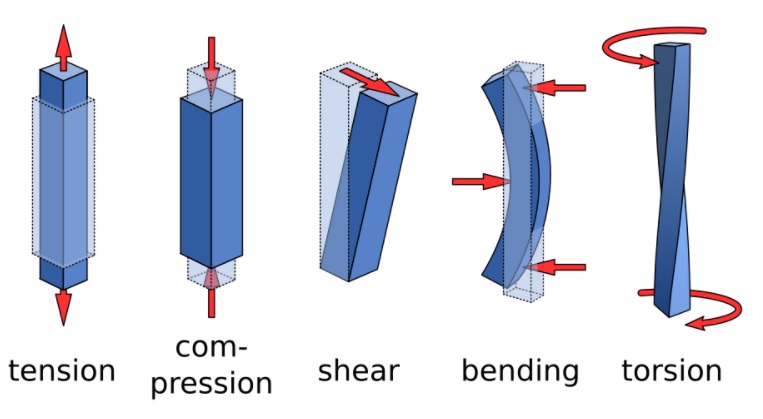
Any functioning component, such as machine parts, structural members, pressure vessels, and so on, are all under the influence of more than one force. When anybody is under the influence of more than one force such as shear forces, bending moments, axial forces, torsion, and so on, then such body is said to be under combined loading. A very practical example of combined loading is the crankshaft of an internal combustion engine (IC engine). The crankshaft of the IC engine is under high rpm, which is caused due to the torsional forces. Due to the presence of piston, counterbalances, and internal imbalances, the crankshaft experiences lateral forces and due to the rise in temperature, the crankshaft undergoes thermal expansion, which pulls the crankshaft along the axial direction and lateral direction. The presence of unbalanced loads along the periphery of the crankshaft also induces a bending moment.
Combined bending and torsion
The stresses that are induced inside the material are known as uniaxial stresses, which occur when the machine components are under the action of only torsion, bending, axial loads, and bending moment. In actual practice, machine components are subjected to a combined state of loadings as in the power transmission shaft of an automobile, which comes under a combined bending of bending moment and torsional loads. Under such conditions, the component experiences a complex state of stress. The stresses are distributed infinitely throughout the material of the component. In a more technical term, these stresses are distributed over multiple planes throughout the component. In design point, determination of these stresses is of immense priority to know the critical planes, which may also lead to component failure along these planes.
Whenever anybody is subjected to a pair of concentrated moments at the extreme ends of the component, the body undergoes bending, and the concentrated moments are known as bending moments, which give rise to bending stresses. For a pair of torsional moments, the body experiences shear stresses.
The bending stress that acts at any fiber of a component under bending moment is given by,
Where, = Bending stress
= Bending moment about the neural axis of the component
= Moment of inertia about the centroidal axis of the component
= Distance of the fiber from the neutral axis
While the shear stress at any point of a cylindrical component under torsional loading can be given as,
Where, = The shear stress acting at any point of the component
= The torsional load or the torque acting on the component
= Radius of the component
= Polar moment of inertia of the component
The maximum amount of shear stress acting on a component due to combined load of bending and torsion can be given by the expression,
, where denotes maximum shear stress
Principal stress and normal stress
The state of stress associated with the material of the component always acts at a point where these stresses have a different orientation. These stresses can be resolved into their respective components that act along the three mutually perpendicular planes. The stresses that act normal to the plane are termed principal stresses and the corresponding plane is known as a principal plane. These principal stresses are also known as normal stresses. The value of the largest principal stress is known as major principal stress and the smallest stress is known as minor principal stress.
The magnitudes of major and minor principal stresses can be determined from the following expression,
Where = Major principal stress
= Minor principal stress
= Stresses acting along the x and y direction respectively due to combined loading
= Stress acting at x face along the y-direction
Principle of superposition
According to the principle of superposition, when a material or a structural member is under the effect of two or more loadings then the effect of the overall loadings can be determined by adding individually, that is, the sum of the effect of the individual loads including the proper sign convention for the individual loads. The principle of superposition is applicable to all types of loading, which the member is subjected to. For instance, bending moments, torsional loadings, axial loadings, and shear loadings.
Context and Applications
This topic is of immense importance in the machine design sector in the industrial domain and structural engineering sector. Besides, the topic is taught extensively as a subject in mechanical engineering and civil engineering courses.
- Bachelors in Technology (Mechanical)
- Bachelors in Technology (Civil)
- Bachelors in Technology (Industrial Designing)
- Masters in Technology (Mechanical)
- Masters in Technology (Civil)
Practice Problems
1. Which of the following is true for combined loading?
- The member is only acted upon by shear loading
- The member is only acted upon by shear and axial loading
- The member is only acted upon by twisting and bending moment
- The member is acted upon by bending and twisting moment, axial loads, and shear loads
Correct option- d
Explanation: During combined loading, the member experiences twisting and bending moments, axial loads, and shear loads. For instance, in an automobile, the crankshaft experiences a twisting moment due to torque applied, a bending moment due to whirling, and an axial load due to thermal expansion and shear loads from bearing reaction.
2. Which of the following stress components acts normal to one of the mutually perpendicular planes?
- Principal stress
- Normal stress
- Shear stress
- Both a and b are correct.
Correct option- d
Explanation: The component of stress which acts normal to one of the mutually perpendicular planes is known as principal stress; it is also known as normal stress.
3. Which of the following is the correct statement for the principle of superposition?
- The effect of all the loads in a member is equal to multiple of individual loads.
- The effect of all the loads in a member is equal to the resultant of the loads.
- The effect of all the loads in a member is equal to the resultant of the loads acting through the centroid of the cross-section.
- The effect of all the loads in a member is equal to the summation of all the loads acting on the member.
Correct option- d
Explanation: The principle of superposition states that the effect of all the loads acting in a member is equal to the summation of all the loads acting either to the right or left of the member.
4. If a machine component is under the action of only bending, torsion, or axial loading, which of the following stresses are induced?
- Triaxial stress
- Biaxial stress
- Uniaxial stress
- Complex stress
Correct option- c
Explanation: When a machine component is under the action of only torsion, bending, axial, shear, and so on, a uniaxial state of stresses is induced.
5. Complex state of stress is induced under which of the following loading conditions?
- Static loading
- Dynamic loading
- Shear loading
- Combined loading
Correct option- d
Explanation: Complex stresses are induced under the action of combined loading.
Want more help with your mechanical engineering homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.
Combined Loading Homework Questions from Fellow Students
Browse our recently answered Combined Loading homework questions.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.