A political analyst believes that a senator's recent decision to support a bill resulted in a drop of approval ratings. To test this claim, he selects random cities in the state that voted the senator in and compares the approval ratings before the decisiorn to the approval ratings after the decision. Suppose that data were collected for a random sample of 8 cities, where each difference is calculated by subtracting the percent approval rating before the decision from the percent approval rating after the decision. Assume that the percentages are normally distributed. Identify the critical value(s) of the t-test statistic, where α-0.05. Use a comma and a space to separate answers as needed 0.01 Probability Degrees of Freedom 5 6 0.10 0.05 0.025 0.005 1.476 1.440 1.415 1.397 1.383 1.372 1.363 1.356 1.350 1.345 1.341 2.015 1.943 1.895 1.860 1.833 1.812 1.796 1.782 2.571 2.447 2.365 2.306 2.262 2.228 2.201 2.179 2.160 2.145 2.131 3.365 3.143 2.998 2.896 2.821 2.764 2.718 2.681 2.650 2.624 2.602 4.032 3.707 3.499 3.355 3.250 3.169 3.106 3.055 3.012 2.977 2.947 1.761 1.753
A political analyst believes that a senator's recent decision to support a bill resulted in a drop of approval ratings. To test this claim, he selects random cities in the state that voted the senator in and compares the approval ratings before the decisiorn to the approval ratings after the decision. Suppose that data were collected for a random sample of 8 cities, where each difference is calculated by subtracting the percent approval rating before the decision from the percent approval rating after the decision. Assume that the percentages are normally distributed. Identify the critical value(s) of the t-test statistic, where α-0.05. Use a comma and a space to separate answers as needed 0.01 Probability Degrees of Freedom 5 6 0.10 0.05 0.025 0.005 1.476 1.440 1.415 1.397 1.383 1.372 1.363 1.356 1.350 1.345 1.341 2.015 1.943 1.895 1.860 1.833 1.812 1.796 1.782 2.571 2.447 2.365 2.306 2.262 2.228 2.201 2.179 2.160 2.145 2.131 3.365 3.143 2.998 2.896 2.821 2.764 2.718 2.681 2.650 2.624 2.602 4.032 3.707 3.499 3.355 3.250 3.169 3.106 3.055 3.012 2.977 2.947 1.761 1.753
Holt Mcdougal Larson Pre-algebra: Student Edition 2012
1st Edition
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Chapter11: Data Analysis And Probability
Section11.4: Collecting Data
Problem 6E
Related questions
Question
Critical Values=
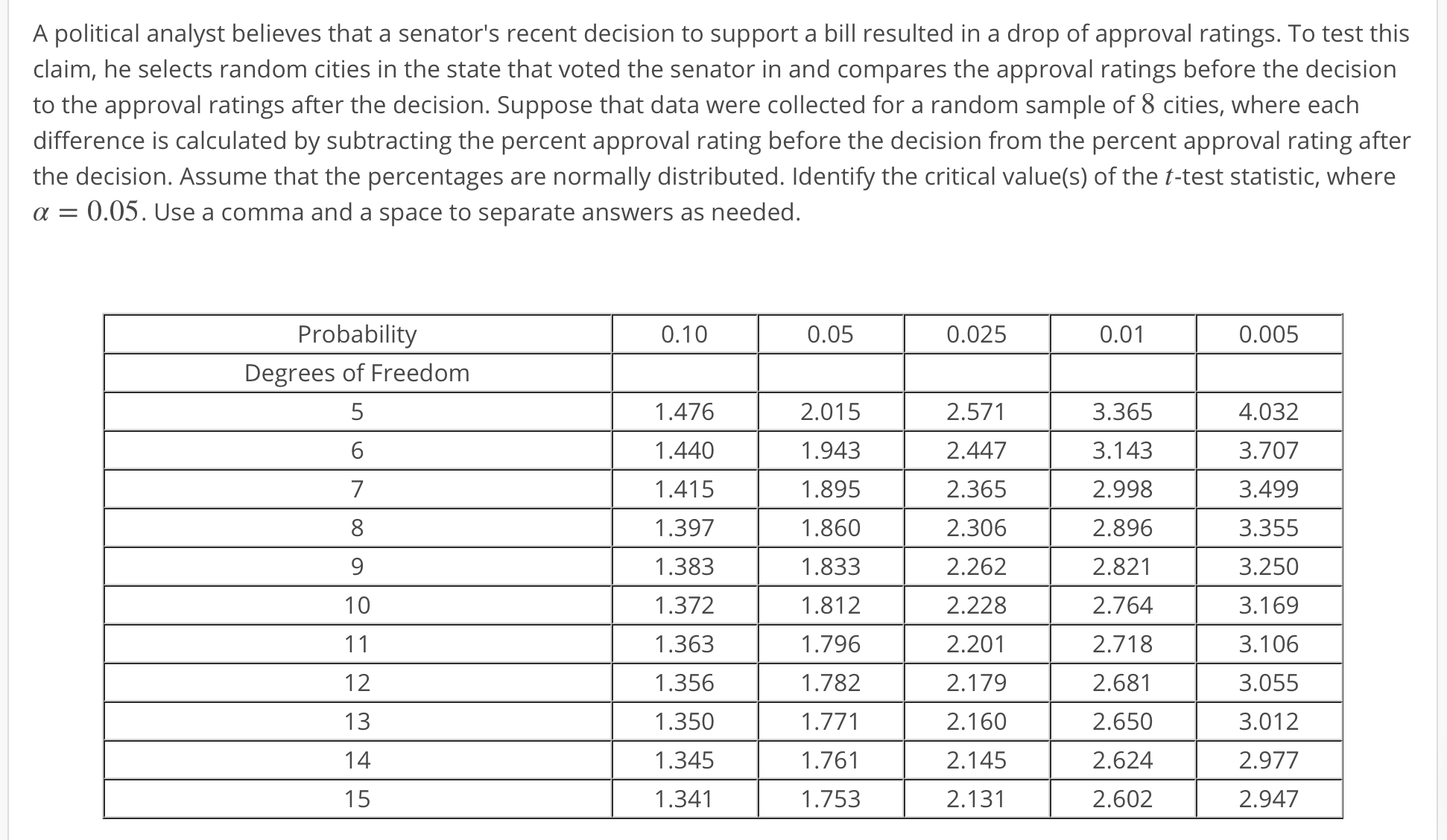
Transcribed Image Text:A political analyst believes that a senator's recent decision to support a bill resulted in a drop of approval ratings. To test this
claim, he selects random cities in the state that voted the senator in and compares the approval ratings before the decisiorn
to the approval ratings after the decision. Suppose that data were collected for a random sample of 8 cities, where each
difference is calculated by subtracting the percent approval rating before the decision from the percent approval rating after
the decision. Assume that the percentages are normally distributed. Identify the critical value(s) of the t-test statistic, where
α-0.05. Use a comma and a space to separate answers as needed
0.01
Probability
Degrees of Freedom
5
6
0.10
0.05
0.025
0.005
1.476
1.440
1.415
1.397
1.383
1.372
1.363
1.356
1.350
1.345
1.341
2.015
1.943
1.895
1.860
1.833
1.812
1.796
1.782
2.571
2.447
2.365
2.306
2.262
2.228
2.201
2.179
2.160
2.145
2.131
3.365
3.143
2.998
2.896
2.821
2.764
2.718
2.681
2.650
2.624
2.602
4.032
3.707
3.499
3.355
3.250
3.169
3.106
3.055
3.012
2.977
2.947
1.761
1.753
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.Recommended textbooks for you

Holt Mcdougal Larson Pre-algebra: Student Edition…
Algebra
ISBN:
9780547587776
Author:
HOLT MCDOUGAL
Publisher:
HOLT MCDOUGAL

College Algebra (MindTap Course List)
Algebra
ISBN:
9781305652231
Author:
R. David Gustafson, Jeff Hughes
Publisher:
Cengage Learning

Holt Mcdougal Larson Pre-algebra: Student Edition…
Algebra
ISBN:
9780547587776
Author:
HOLT MCDOUGAL
Publisher:
HOLT MCDOUGAL

College Algebra (MindTap Course List)
Algebra
ISBN:
9781305652231
Author:
R. David Gustafson, Jeff Hughes
Publisher:
Cengage Learning