What is Average? 

In mathematics, everyone must have heard the term average in one place or other. Almost all types of calculation require taking out an average. In everyday life, the term is used for denoting a certain amount that can be said to be a typical quantity for multiple people or objects. In other words, if a group of people possesses a certain object, then the average gives us an idea regarding the quantity of the object possessed by each person. However, this is solely based on mathematical calculation. It is important to note that most people will not strictly have the average value in a group. 

Real-Life Example of Average 

In a real-life scenario, suppose the average height of a group of 10 high school students is 160 cm. However, that does not mean that each of the 10 students has a height exactly equal to 160 cm. Now, there will be students who are taller than 160 cm, and there will also be students who are shorter than the said height. In this case, the average gives us a rough idea about how tall the students of this group can be. When we generalize it, we can get the normal expectation of the height for all the students. 

How does Average Work?

The concept of average is quite ancient. From old times, people have tried to estimate a quantity that can give a general quantitative idea about a group of similar products. For instance, all of us are familiar with terms like the average marks scored by students, the average income of a man, or the average performance of a sportsperson. 

Taking the above example in consideration, let us say the heights of 10 students are as follows- 

150 cm, 153 cm, 155 cm, 157 cm, 159 cm, 161 cm, 163 cm, 165 cm, 167 cm, 170 cm 

The total of their heights is (150 + 153 + 155 + 157 + 159 + 161 + 163 +165 +167 + 170)  cm, which equals 1600 cm. Here, the total number of students is 10. 

We can find out the average by the following formula- 

$\text{Average = }\frac{\text{Total sum of the quantity of the items}}{\text{no}\text{. of items}}$

We use this formula in the above example to find the average. 

Therefore, average = 1600/10 = 160 cm. 

Similarly, we see the average in the diagram below. 

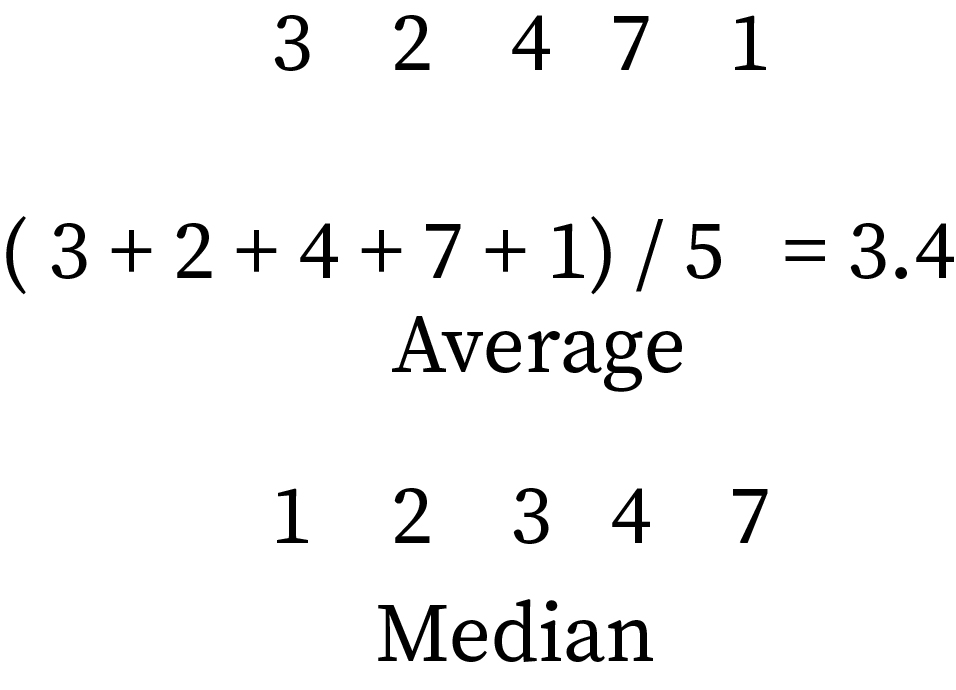
This is the method for finding out the plain average of any group of items. 

It is to note that the quantities should have the same unit before their average is calculated. If not, their units should all be converted to match each other. 

For instance, if the height of one student was given as 1.7 m, and the heights of other students are given in cm, then it should be converted to 170 cm before taking the average. 

In other terms, an average is also known as a mean. The mean or average is used to find out the quantity that can describe or generalize a large group of items or products. When calculations are done on a large scale, it is not always possible to cater to each item individually. Hence, we get a general quantitative idea of all items using the average value, and we can take the measures accordingly. 

How to Find the Average of Multiple Groups?

In real-life situations, we may need to calculate the average of more than one group at the same time. Here, normal equations of average do not work. However, the concept remains the same. 

If we need to find out the average of two groups, then these two groups are combined to form a third group. The average is found out of this third group instead. This is one of the best solutions for finding out the average of multiple groups at the same time. 

For instance, if the 1^st group contains ‘p’ items, and the 2^nd group contains ‘q’ items, then the total number of items equals ‘p + q’ for the combined group. Let the average of the 1^st group and the 2^nd group be ‘a’ and ‘b’ respectively. Also, let the combined average be ‘A’. In this case, the sum of the items in the 1^st group will be ‘pa’. Similarly, the sum of items in the 2^nd group will be ‘qb’. The combined sum of the items will be ‘pa + qb’. 

Here, we can say that the combined average A is- 

$A=\frac{\left(pa+qb\right)}{\left(p+q\right)}$

When more than two groups are taken into consideration, then similar formula works to calculate the average. 

How do Addition and Subtraction of Items Affect the Average?

With the change in the number of items, the average will surely get changed as well. It can either increase or decrease, depending upon whether items are added or removed. 

When items are added 

If there are M items with an average K, and m new items are added, then, let the sum of new values equal x. 

Therefore, the new average will be calculated by- 

$NewAverage=K+\frac{x-K}{M+m}$

When items are removed 

We consider that there are M items with an average K, and m items are removed, then, let the sum of removed values be x. 

Similarly, the new average becomes- 

$NewAverage=K+\frac{K-x}{M-m}$

Notice that the signs in the two terms changed. 

How to Replace Items in Average?

By replacement of items in an average, we mean that some of the items are removed initially from the group, and then different items are added in the group. It is to be noted that the number of items removed is always equal to the number of items added. That is how the replacement occurs. If not, the total number of items will change, and we have already discussed this case above. 

When items are replaced, the initial average will obviously be affected. Let the change in the average is y. If there are a total of ‘X’ items, then the sum of the added items subtracted from the sum of the removed items will equal (+ or -) Xy. We use ‘+’ when the average gets increased, and use ‘-‘, when there is a decrease in the average after the replacement of items. 

Practice Problem

Q) Let there be a group of 10 people. When a man who weighs 100 kg gets replaced by another man, the average weight reduces by 5 kg. Find out the weight of the new man. 

Solution :

According to the problem, 

New man’s weight – removed man’s weight = - Xy 

Here, X =10, y = 5, and we use ‘-‘, as the average weight decreases. 

Therefore, we get  

New man’s weight – 100 = - 10 * 5 

New man’s weight = 100 – 50 = 50 

Hence, the new man weighs 50 kg, which is the required answer. 

Formulas 

The average of a group is calculated as: 

$\text{Average = }\frac{\text{Total sum of the quantity of the items}}{\text{no}\text{. of items}}$

If there are ‘p’ items in a group having an average ‘a’ and ‘q’ items in another group having an average ‘b’, then the combined average of the two groups is evaluated as: 

$A=\frac{\left(pa+qb\right)}{\left(p+q\right)}$

Context and Applications: 

This topic is significant in the professional exams for both undergraduate and graduate courses, especially for  

• Bachelor of Science in Mathematics 
• Master of Science in Mathematics