cosh (-2x)
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Use the Taylor Series in Table 11.5 to find the first four nonzero terms of the Taylor Series for the following functions centered at 0.

Transcribed Image Text:Table 11.5 asserts, without proof, that
in several cases, the Taylor series for
f converges to f at the endpoints of
the interval of convergence. Proving
Table 11.5
1
= 1 + x + x² +
1- x
+ x* +
Ert, for |x| < 1
... -
k=0
convergence at the endpoints generally
requires advanced techniques. It may also
be done using the following theorem:
Suppose the Taylor series for f
centered at 0 converges to f on the
interval (-R, R). If the series converges
at x = R, then it converges to lim f(x).
1
= 1 - x + x² .
- E(-1)x*, for [x| < 1
- ..·+ (-1)*x* + • · · =
|
1 + x
k=0
for |x| < 0
k!
e = 1 + x +
+
+
+
... -
2!
k!
k=0
(-1)*x*+1
(2k + 1)!
(-1)*x*+1
(2k + 1)!
sin x = x –
+
for x < 0
+... =
If the series converges at x = -R, then it
3!
5!
k=0
converges to lim f(x).
x--R+
(-1)*x*
Σ
(2k)!
(-1)* x*
2k
x2
+
2!
00
For example, this theorem would
for |x| < ∞
cos x = 1
+...=
allow us to conclude that the series for
4!
(2k)!
k=0
In (1 + x) converges to In 2 at x = 1.
x?
In (1 + x) = x -
(-1)*+1 *
+
(-1)*+'*
Σ
for -1 < x< 1
+... =
3
k
k=1
-In (1 – x) :
x?
= x +
+
+
k
for -1 < x < 1
3
k=1
(-1)*x*+1
(-1)* x*+1
-1
tan
Σ
2k + 1
for |x| < 1
n¯'x = x -
+
+...=
3
2k + 1
k=0
x2k+1
Σ
k=o(2k + 1)!’
x2k+1
sinh x = x +
3!
for x < 0
+...=
5!
(2k + 1)!
cosh x = 1 +
+
4!
Σ
for x < 0
+... =
(2k)!
(2k)!
k=0
p(p – 1)(p – 2) · ·· (p – k + 1) (P) :
As noted in Theorem 11.6, the binomial
series may converge to (1 + x)® at
x = ±1, depending on the value of p.
(2)
...
(1 + x)" =
Σ
x*, for x < 1 and
= 1
k!
=0
+
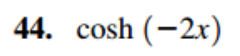
Transcribed Image Text:44. cosh (-2x)
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 2 steps

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

