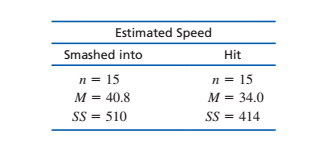
Estimated Speed Smashed into Hit n = 15 n = 15 M = 40.8 M = 34.0 %3D SS = 414 SS = 510 %3!
10. In 1974, Loftus and Palmer conducted a classic study demonstrating how the language used to ask a question can influence eyewitness memory. In the study, college students watched a film of an automobile accident and then were asked questions about what they saw. One group was asked, “About how fast were the cars going when they smashed into each other?” Another group was asked the same question except the verb was changed to “hit” instead of “smashed into.” The “smashed into” group reported significantly higher estimates of speed than the “hit” group. Suppose a researcher repeats this study with a sample of today’s college students and obtains the following results.
a. Do the results indicate a significantly higher estimated speed for the “smashed into” group? Use a one-tailed test with α = .01.
b. Compute the estimated value for Cohen’s d to measure the size of the effect.
c. Write a sentence demonstrating how the results of the hypothesis test and the measure of effect size would appear in a research report.
Trending now
This is a popular solution!
Step by step
Solved in 5 steps with 2 images








