Heteroskedasticity arises because of non-constant variance of the error terms. We said proportional heteroskedasticity exists when the error variance takes the following structure: Var(et)=σt^2=σ^2 xt. But as we know, that is only one of many forms of heteroskedasticity. To get rid of that specific form of heteroskedasticity using Generalized Least Squares, we employed a specific correction – we divided by the square root of our independent variable x. And the reason why that specific correction worked, and yielded a variance of our GLS estimates that was sigma-squared, was because of the following math: (Picture 1) Where var(et)=σ^2 according to our LS assumptions. In other words, dividing everything by the square root of x made this correction work to give us sigma squared at the end of the expression. But if we have a different form of heteroskedasticity (i.e. a difference variance structure), we have to do a different correction to get rid of it. (a) what correction would you use if the form of heteroskedasticity you encountered was assumed to be each of the following? Show ma
Heteroskedasticity arises because of non-constant variance of the error terms. We said proportional heteroskedasticity exists when the error variance takes the following structure: Var(et)=σt^2=σ^2 xt.
But as we know, that is only one of many forms of heteroskedasticity. To get rid of that specific form of heteroskedasticity using Generalized Least Squares, we employed a specific correction – we divided by the square root of our independent variable x. And the reason why that specific correction worked, and yielded a variance of our GLS estimates that was sigma-squared, was because of the following math: (Picture 1)
Where var(et)=σ^2 according to our LS assumptions. In other words, dividing everything by the square root of x made this correction work to give us sigma squared at the end of the expression. But if we have a different form of heteroskedasticity (i.e. a difference variance structure), we have to do a different correction to get rid of it.
(a) what correction would you use if the form of heteroskedasticity you encountered was assumed to be each of the following? Show mathematically (like the equation above does) why the correction you are suggesting would work.
(Picture 2)
(b) using the household income/food expenditure data found the dataset below, use GLS to estimate our model employing the corrections (one model for each correction) you suggested in part (a) above. Fully report your results.
(c) use the Goldfeldt-Quandt test to determine whether your corrections worked from the previous question were successful. Be sure to carry out all parts of the hypothesis tests. Based upon the results of your GQ tests, which of your two corrections do you think works better?
Dataset:
| Food Exp | Wkly Income |
| 52.25 | 258.3 |
| 58.32 | 343.1 |
| 81.79 | 425 |
| 119.9 | 467.5 |
| 125.8 | 482.9 |
| 100.46 | 487.7 |
| 121.51 | 496.5 |
| 100.08 | 519.4 |
| 127.75 | 543.3 |
| 104.94 | 548.7 |
| 107.48 | 564.6 |
| 98.48 | 588.3 |
| 181.21 | 591.3 |
| 122.23 | 607.3 |
| 129.57 | 611.2 |
| 92.84 | 631 |
| 117.92 | 659.6 |
| 82.13 | 664 |
| 182.28 | 704.2 |
| 139.13 | 704.8 |
| 98.14 | 719.8 |
| 123.94 | 720 |
| 126.31 | 722.3 |
| 146.47 | 722.3 |
| 115.98 | 734.4 |
| 207.23 | 742.5 |
| 119.8 | 747.7 |
| 151.33 | 763.3 |
| 169.51 | 810.2 |
| 108.03 | 818.5 |
| 168.9 | 825.6 |
| 227.11 | 833.3 |
| 84.94 | 834 |
| 98.7 | 918.1 |
| 141.06 | 918.1 |
| 215.4 | 929.6 |
| 112.89 | 951.7 |
| 166.25 | 1014 |
| 115.43 | 1141.3 |
| 269.03 | 1154.6 |
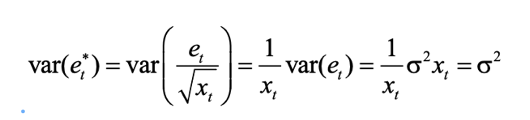
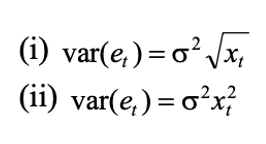
Trending now
This is a popular solution!
Step by step
Solved in 7 steps with 2 images




