Physics for Scientists and Engineers: Foundations and Connections
1st Edition
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Katz, Debora M.
Chapter25: Gauss’s Law
Section: Chapter Questions
Problem 2PQ
Related questions
Question
Two long, parallel wires
separated by a distance 2d carry
equal currents in the same direction.
An end view of the two wires
is shown in Figure P19.54, where
the currents are out of the page.
(a) What is the direction of the
magnetic field at P on the x - axis
set up by the two wires? (b) Find an
expression for the magnitude of the
field at P. (c) From your result to part (b), determine the field
at a point midway between the two wires. Does your result
meet with your expectation? Explain.
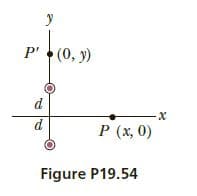
Transcribed Image Text:P'(0, y)
P (x, 0)
Figure P19.54
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 4 steps with 4 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Recommended textbooks for you

Physics for Scientists and Engineers: Foundations…
Physics
ISBN:
9781133939146
Author:
Katz, Debora M.
Publisher:
Cengage Learning

Physics for Scientists and Engineers: Foundations…
Physics
ISBN:
9781133939146
Author:
Katz, Debora M.
Publisher:
Cengage Learning