What is Magnetic Force?
A magnetic force arises when a charged particle or a current-carrying conductor is placed in a magnetic field. It is created because of the movement of the charged particles.
Consider an electrical wire having charged particles that are moving with velocity (v) in a magnetic field (B). Magnetic force refers to the interaction between the magnetic field induced by the moving particles and the applied magnetic field. Here, the charge (q) experiences magnetic force. The total force acting on the electrical wire is,
Where,
is the force due to the electric field
is the force due to the magnetic field
What is a Magnet?
A magnet is a material or substance that is used to produce a magnetic field in the region surrounding the material. A magnet has two poles, a north pole and a south pole. Like poles repel each other and unlike poles attract each other.
A magnet will attract ferromagnetic materials, like iron (Fe), nickel (Ni), and cobalt (Co). Materials like wood, cotton, and plastic don’t have a magnetic field.
How to Find Magnetic Force
Let us take a two-point charge that has magnitudes of magnetic force connecting the particles. The magnetic force depends on the number of charges and motions in each of two point charges and how far apart they are. The direction of the force depends on the relative motions of a charge.
Here, the positive charge (q) moves with unvarying magnetic field (B) having a velocity (v). The angle amid the magnetic field and velocity is θ. Thus, the magnetic force observed by the charged particle depends on the below factors.
1. The magnitude of the force observed by the charge is directly proportional to its magnitude.
2. The magnitude of the force, F, is directly proportional to its velocity, v, which acts on the perpendicular directions of the magnetic field.
3. The magnitude of the force is directly proportional to the magnitude of its applied magnetic force.
Comparing the equations (1), (2) & (3), we get,
Now rewriting the above equation,
Where,
k is a proportionality constant (k=1).
Now, the equation may be rewritten as,
In vector terms,
Here, v=1, q=1, and sin θ=1,
then,
F=B
The above expression describes that a magnetic field induction at a point on a magnetic field equals the force observed by its unit charge moving with the unit velocity, which is perpendicular to the directions of the magnetic field.
Lorentz Force
Lorentz force describes the combination of electric field and magnetic field on point charges of magnetic force. The force applied on a charged particle (q) makes it move with a velocity (v) through a magnetic field (B) and electric field (E). The entire electromagnetic force (F) on the charged particles is called Lorentz force.
Lorentz force can be described as,
Where,
F is a force that acts on the charged particle.
q is a charge of the particle.
v is the velocity of a particle.
E is the electric field.
B is the magnetic field.
Fleming's Left-Hand Rule
Fleming's left-hand rule describes some special cases when the charge observes maximum forces. If we stretch the thumb finger, central finger, and index finger of the left hand in such a way to make an angle of 90 degrees, they lie perpendicular to each other. These fingers represent the direction of a magnetic field & velocity.
- The index finger or first finger shows the directions of a magnetic field.
- The middle finger shows the directions of motion of electric charge.
- The thumb finger shows the force observed by the charged particle.
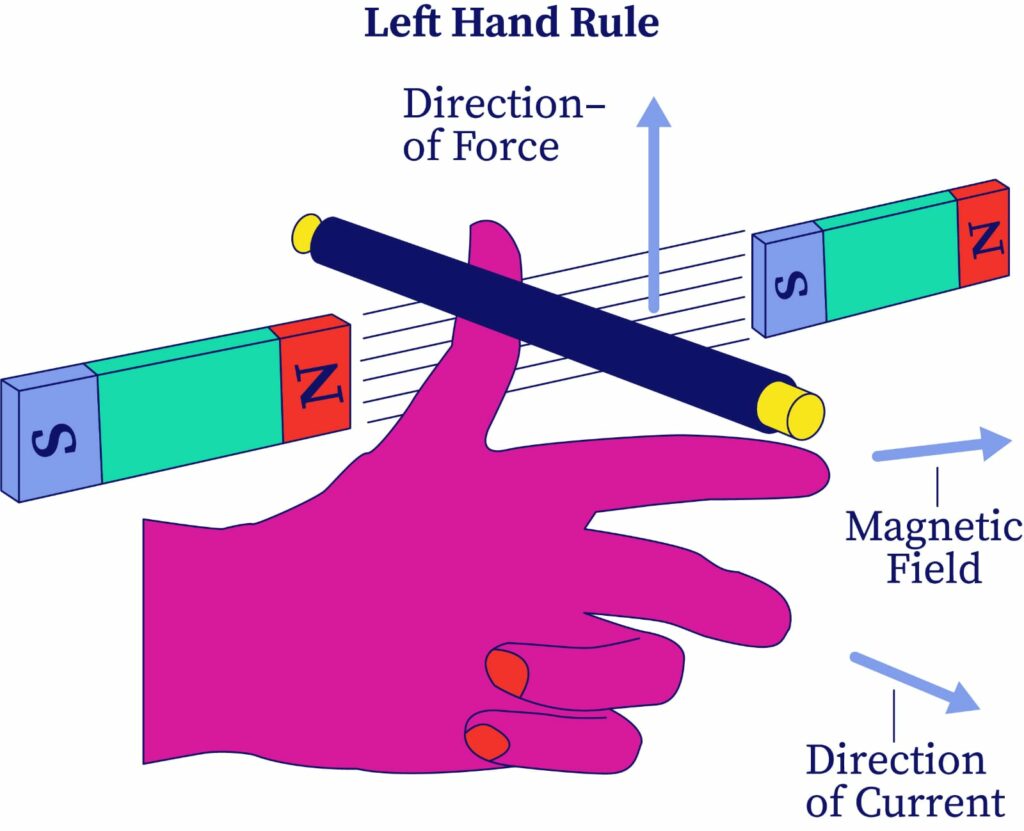
If the velocity lies on the x-axis, a magnetic field lies on the y-axis and a magnetic force lies on the z-axis.
Magnetic Force on a Current-Carrying Wire
Let us take a current-carrying conductor or wire. The force enclosed by the conductor or wire is due to its magnetic field. When charged particles move below the magnetic field, there are some forces that are perpendicular to the charged particle's movement. The length of a wire or conductor is l and the cross-sectional area is A. In the current carrying conductor or wire, the number of moving electrons is taken to be n.
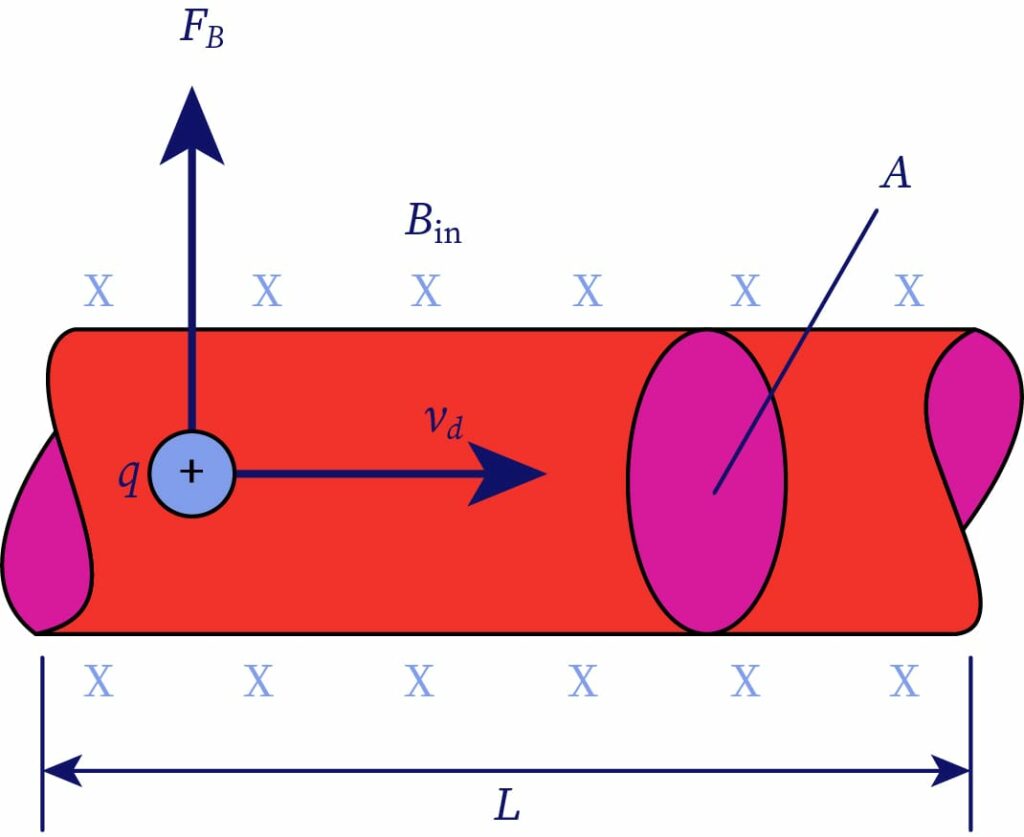
Henceforth, the total number of charged particles is described by , where I is a stable current flow in a conductor or wire. The drift velocity of every moving electron is represented by The current-carrying conductor is kept at a magnetic field, B. Thus, the applied magnetic force on moving electrons can be expressed as,
Where,
q is a value of moving charge carriers or electrons.
Uses of Magnetic Force
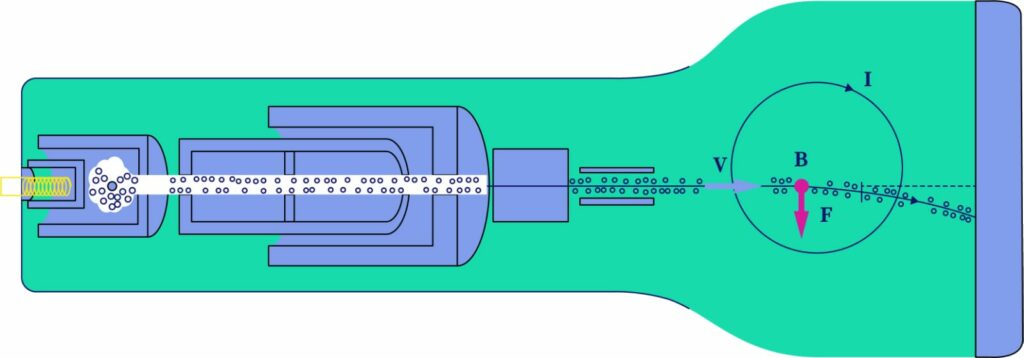
Mass Spectrometer
Mass spectrometers are widely used to determine the composition, properties, and chemical structure for different materials with the help of a magnetic field (or magnetism) and electric field.
Cathode Ray Tube (CRT)
The electron rays from the CRT are generated at the electron gun present in the cathode. Two pairs of magnetic coils are used to direct the electrons in a vertical direction and another one in the horizontal direction to reach a designation. These CRT tubes are used in many old televisions, oscilloscopes, and computer monitors.
Magnetic Resonance Imaging (MRI)
Magnetic resonance imaging is an essential technique used in the medical field. It is used to image internal organs and tissues due to their magnetism.
Ferromagnetism
Ferromagnetic materials play a vital role in trending technology. Due to their high magnetism, these ferromagnetic materials are used in sensors, hard drives, magnetic tape recorders, transformers, speakers, etc.
Compass
A compass is a tool or device to determine direction as a result of a magnetic field. A pin-type magnetic needle placed on the compass moves freely to face in the direction of north or south.
Electric Motor
In our day-to-day lives, we use hairdryers, trimmers, and electric razors, all of which work with the help of a magnetic force. Here, electric motors convert electrical energy into magnetic fields with the help of a coil. A magnetic field creates a magnetic force that enables the motor to function.
Formulas
The Lorentz force equation is given by,
Magnitude of the magnetic force is given by,
Context and Applications
This topic is one of the crucial applications in all forms of classical mechanics and it is significant for both undergraduate and postgraduate courses, especially for:
- Bachelors in Science (Physics)
- Masters in Science (Physics)
Practice Problems
1. A charged particle (q) is moving with a steady magnetic field (B) having a velocity of of m/s. The angle between the magnetic field and velocity is 25º. Find the magnetic force that acts on the charged particles. Here, q=3 µC and B=100 G.
a.
b.
c.
d.
Answer: a
Given data:
q=3 µC
B=100 G
v= m/s
θ=25°
Explanation:
The magnitude of the magnetic force acting on a mobile carrier is devised by the below formula:
The magnetic force acting on a mobile carrier is
2. When current charges move in the same direction in two conductors, then the force is __________.
a. Repulsive
b. Attractive
c. Opposing
d. Retracting
Answer: b
Explanation: When two conductors have charged particles moving in the same direction, then the forces of the two conductors will be directed toward each other.
3. The space around a current-carrying conductor, in which its magnetic effect can be experienced, is the ________.
a. Electric pole
b. Electric field
c. Magnetic pole
d. Magnetic field
Answer: d
Explanation: When a current passes through a conductor, it modifies the space around the conductor and forms a magnetic field.
4. What is the force exerted by a stationary charge when it is placed in a magnetic field?
a. Maximum
b. Zero
c. Minimum
d. None of the above
Answer: b
Explanation: A stationary charge does not produce any magnetic field and does not suffer any interaction against the external magnetic field. Hence, the force exerted is zero.
5. Find the magnetic force on a charge 2.5 C with a flux density of 3 units having a velocity of 2 m/s.
a. 20 units
b. 15 units
c. 28 units
d. 30 units
Answer: b
Given data:
The charge (q) = 2.5 C
The flux density (B) =3 units
The velocity (v) = 2 m/s
Explanation:
The magnitude of the magnetic force is given by,
The magnetic force is 15 units.
Want more help with your physics homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Magnetic Force Homework Questions from Fellow Students
Browse our recently answered Magnetic Force homework questions.