Angular Impulse and Momentum Principles
To apply the principle of angular impulse and momentum to describe a particle's motion.
The moment of a force about a point O, fixed in an inertial coordinate system, MO, and the angular momentum about the same point, HO, are related as follows:
∑MO=H˙O
where H˙O is the time derivative of the angular momentum, HO=r×mv. Integrating this equation with respect to time yields the following equation:
∑∫t2t1MO dt=(HO)2−(HO)1
This equation is the principle of angular impulse and momentum, and it is often rearranged to its more familiar form
(HO)1+∑∫t2t1MO dt=(HO)2
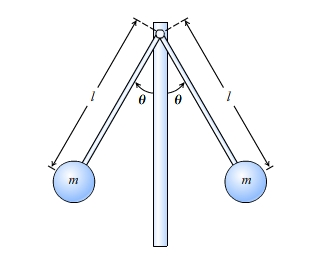
A centrifugal governor consists of a central rotating shaft that has two thin, pin-connected rods attached to it; a heavy sphere caps the end of each rod. (Figure 1) A centrifugal governor
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 3 images









