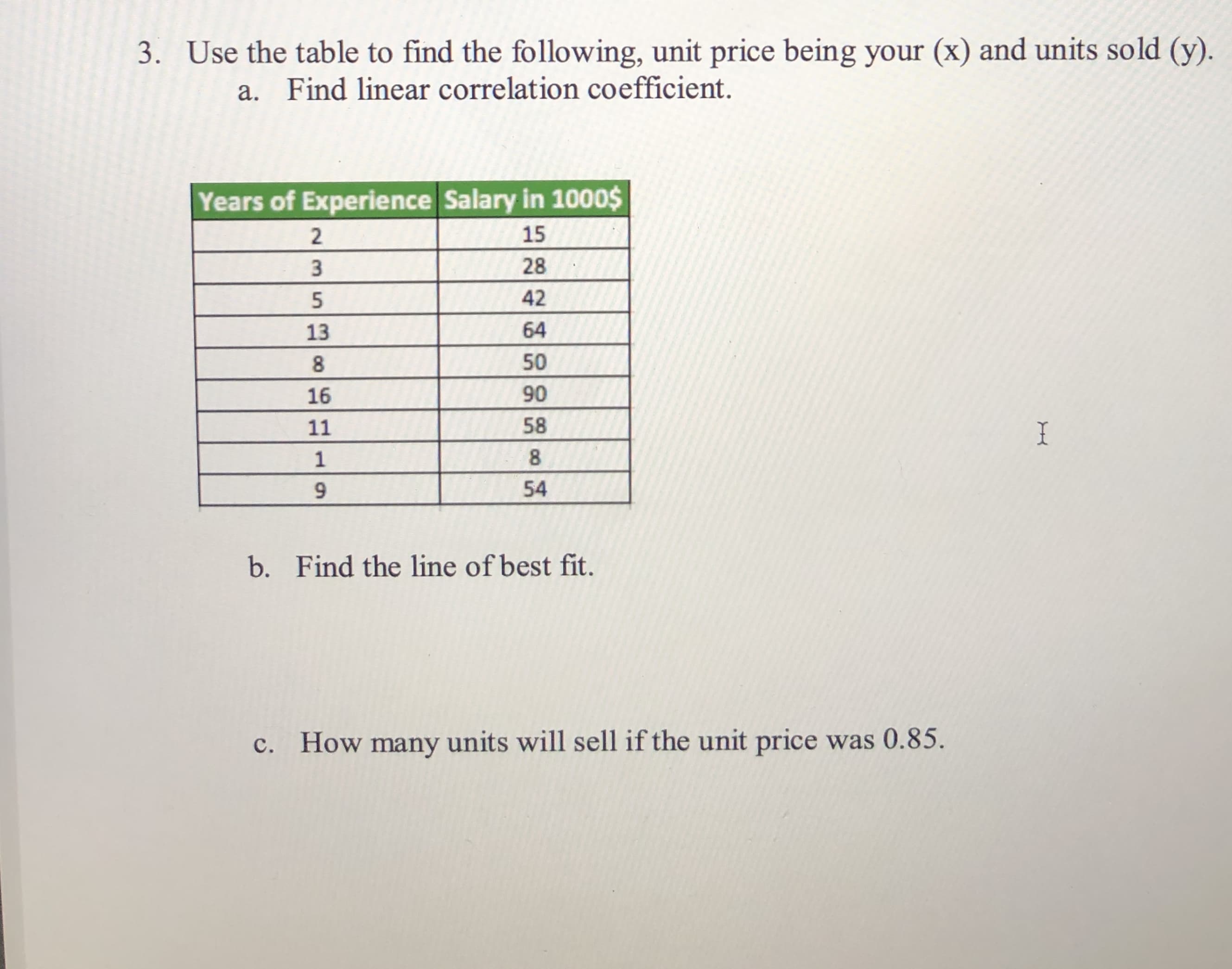
Use the table to find the following, unit price being your (x) and units sold (y). a. Find linear correlation coefficient. Years of Experience Salary in 1000$ 15 3 28 42 13 64 50 16 90 11 58 1 9. 54 b. Find the line of best fit. c. How many units will sell if the unit price was 0.85.

An economist want to determine the relation between one’s FICO score, x, and the interest rate of a 36-month auto loan, y. The given data represent the interest rate (in percent) a bank would offer on a 36-month auto load for various FICO scores. Credit Score;x Interest Rate (percent);y 545 18.982 595 17.967 640 12.218 675 8.612 705 6.68 750 5.15 Find the least-squares regression line treating the FICO score as the explanatory variable and the interest rate as the response variable. Predict the interest rate a person would pay if their FICO score were the median score of 723.

A researcher is interested in whether the variation in the size of human beings is proportional throughout each part of the human. To partly answer this question they looked at the correlation between the foot length (in millimeters) and height (in centimeters) of 30 randomly selected adult males. The data is provided below. Use Excel to calculate the correlation coefficient r between the two data sets. Round your answer to two decimal places. Foot length (mm) Height length (cm) 269.1 188.6 245.7 177.5 272.7 166.9 271.8 155.1 273.9 144.3 274.7 133.8 255.7 122.6 276.5 157.4 279.6 145.9 280.1 135.6 281.9 123.5 HelpCopy to ClipboardDownload CSV

Using the scatter plot of the registered nurse salary data shown, what type of correlation, if any do you think the data have? Explain. Registered Nurses 70 O A. There appears to be a strong positive linear correlation. As the years of experience of the registered nurses increase, salaries tend to decrease. 65 60 O B. There appears to be a strong positive linear correlation. As the years of experience of the registered nurses increase, salaries tend to increase. 55 50 OC. There appears to be a strong negative linear correlation. As the years of experience of the registered nurses increase, salaries tend to decrease. 45 40 O D. There does not appear to be any linear correlation. 2 46 8 10 12 14 16 18 20 22 24 Years of experience O Time Remaining: MacBook Air 80 esc F9 F10 F1 F2 F3 F4 F5 F6 F7 F8 23 $ & 1 7 Annual salary (in thousands) * CO

The following graph plots data for tax per gallon and internal miles.Carefully explain what the graph is about, and what it captures.   What are the limitations of the correlation and what can a researcher do toovercome these?

sub-part 3. please help me with the rest. thanks

The table shows the number of absences, x, in a class and the final exam grade, y, for seven students. X 1 0 2 6 4 3 3 Y 95 90 90 55 70 80 85 Use the graphing calculator to find the correlation coefficient. (Round answer to three decimal places. Do not write 0.123 as.123.)

Identify the reasons the following statements are incorrect. Not all reasons will be used. Researchers found that the correlation between the number of pages in novels and Correlation should depend on units. the number of hours it takes to read them is r = 0.71 pages. The correlation between the advertised selling price of cars and the makes of the Both variables should be numerical. cars is r = -0.69. The amount of ice cream in a sundae and the total grams of fat are highly Correlation should depend on units. correlated (r = 1.15). The correlation between total daily snowfall in inches and daily low temperatures Both variables should be numerical. in degrees Fahrenheit differs from the correlation between daily snowfall in inches and daily low temperatures in degrees Celsius. Answer Bank One of the variables should be categorical. Correlation should not depend on units. Correlation should depend on units. Correlation should be greater than 0. Both variables should be numerical.…

solve last question

Determine the type of direction of correlation that you would expect of the given case / situation. Speed of wind turbines and amount of electricity generated. no correlation positive correlation zero correlation negative correlation