Chemistry: Matter and Change
1st Edition
ISBN:9780078746376
Author:Dinah Zike, Laurel Dingrando, Nicholas Hainen, Cheryl Wistrom
Publisher:Dinah Zike, Laurel Dingrando, Nicholas Hainen, Cheryl Wistrom
Chapter12: States Of Matter
Section: Chapter Questions
Problem 78A
Related questions
Question
Vapor pressure data are given here for octane, C8H18 . Use the Clausius–Clapeyron equation to calculate the molar enthalpy of vaporization of octane and its normal boiling point.
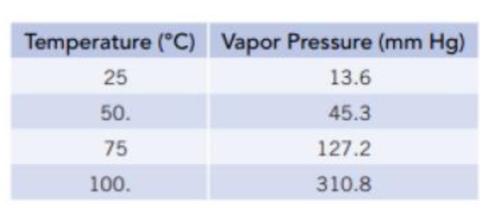
Transcribed Image Text:Temperature (°C) Vapor Pressure (mm Hg)
25
13.6
50.
45.3
75
127.2
100.
310.8
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 4 steps with 1 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, chemistry and related others by exploring similar questions and additional content below.Recommended textbooks for you

Chemistry: Matter and Change
Chemistry
ISBN:
9780078746376
Author:
Dinah Zike, Laurel Dingrando, Nicholas Hainen, Cheryl Wistrom
Publisher:
Glencoe/McGraw-Hill School Pub Co

Introductory Chemistry: An Active Learning Approa…
Chemistry
ISBN:
9781305079250
Author:
Mark S. Cracolice, Ed Peters
Publisher:
Cengage Learning

General Chemistry - Standalone book (MindTap Cour…
Chemistry
ISBN:
9781305580343
Author:
Steven D. Gammon, Ebbing, Darrell Ebbing, Steven D., Darrell; Gammon, Darrell Ebbing; Steven D. Gammon, Darrell D.; Gammon, Ebbing; Steven D. Gammon; Darrell
Publisher:
Cengage Learning

Chemistry: Matter and Change
Chemistry
ISBN:
9780078746376
Author:
Dinah Zike, Laurel Dingrando, Nicholas Hainen, Cheryl Wistrom
Publisher:
Glencoe/McGraw-Hill School Pub Co

Introductory Chemistry: An Active Learning Approa…
Chemistry
ISBN:
9781305079250
Author:
Mark S. Cracolice, Ed Peters
Publisher:
Cengage Learning

General Chemistry - Standalone book (MindTap Cour…
Chemistry
ISBN:
9781305580343
Author:
Steven D. Gammon, Ebbing, Darrell Ebbing, Steven D., Darrell; Gammon, Darrell Ebbing; Steven D. Gammon, Darrell D.; Gammon, Ebbing; Steven D. Gammon; Darrell
Publisher:
Cengage Learning

Introductory Chemistry: A Foundation
Chemistry
ISBN:
9781337399425
Author:
Steven S. Zumdahl, Donald J. DeCoste
Publisher:
Cengage Learning

Chemistry: An Atoms First Approach
Chemistry
ISBN:
9781305079243
Author:
Steven S. Zumdahl, Susan A. Zumdahl
Publisher:
Cengage Learning
