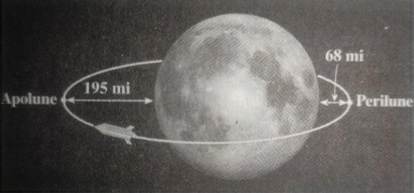
For an object in an elliptical orbit around the moon, the points in the orbit that are closest to and farthest from the center of the moon are called perilune and apolune, repectively. These are the vertices of the orbit. The center of the moon is at one focus of the orbit. The Apollo 11 spacecraft was placed in a lunar orbit with perilune at 68 mi and apolune at 195 mi above the surface of the moon. Assuming that the moon is a sphere of radius 1075 mi, find an equation for the orbit of Apollo 11. (Place the coordinate axes so that the origin is at the center of the orbit and the foci are located on the x-axis)

For an object in an elliptical orbit around the moon, the points in the orbit that are closest to and farthest from the center of the moon are called perilune and apolune, repectively. These are the vertices of the orbit. The center of the moon is at one focus of the orbit. The Apollo 11 spacecraft was placed in a lunar orbit with perilune at 68 mi and apolune at 195 mi above the surface of the moon. Assuming that the moon is a sphere of radius 1075 mi, find an equation for the orbit of Apollo 11. (Place the coordinate axes so that the origin is at the center of the orbit and the foci are located on the x-axis)

Algebra & Trigonometry with Analytic Geometry

13th Edition

ISBN:9781133382119

Author:Swokowski

Publisher:Swokowski

Chapter10: Sequences, Series, And Probability

Section10.2: Arithmetic Sequences

Problem 51E

See similar textbooks