What is a Vertex of an Ellipse?
In the study of the conic section of the geometry, An ellipse is a plane curve surrounding two focal points, or foci where the set of all locus of points in the plane has their sum of the distances to the two foci is constant. On the ellipse curve, it is the intersection point of the main axis. In an ellipse graph, the center of the axis is the midpoint of the line segment connecting the foci. The major axis is the line section that runs through the ellipse's foci, while the minor axis runs through the middle and is perpendicular to the major axis.. The ellipse has two endpoints on the major axis which are known as the vertices (in plural), vertex in the singular. The equation of the major axis is 2a, the equation of the minor is 2b and the distance between the major axis and minor axis is 2c. The semi-major axis has a length of a and the semi-minor axis has a length of b. The ellipse's vertices are determined by the elliptical orbit's equation and graph.
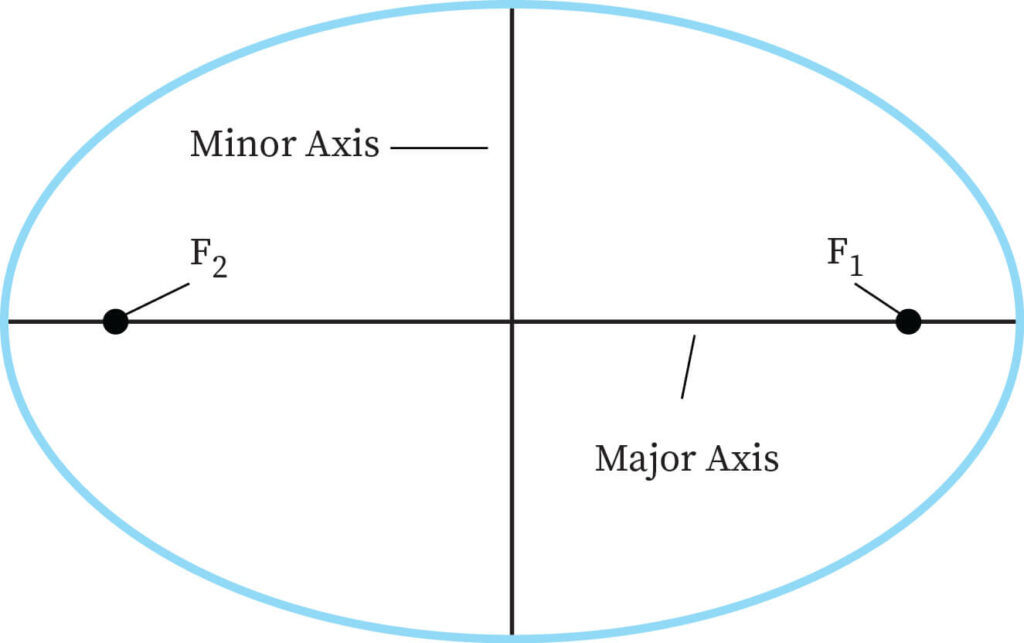
Graph and Equation for an Ellipse
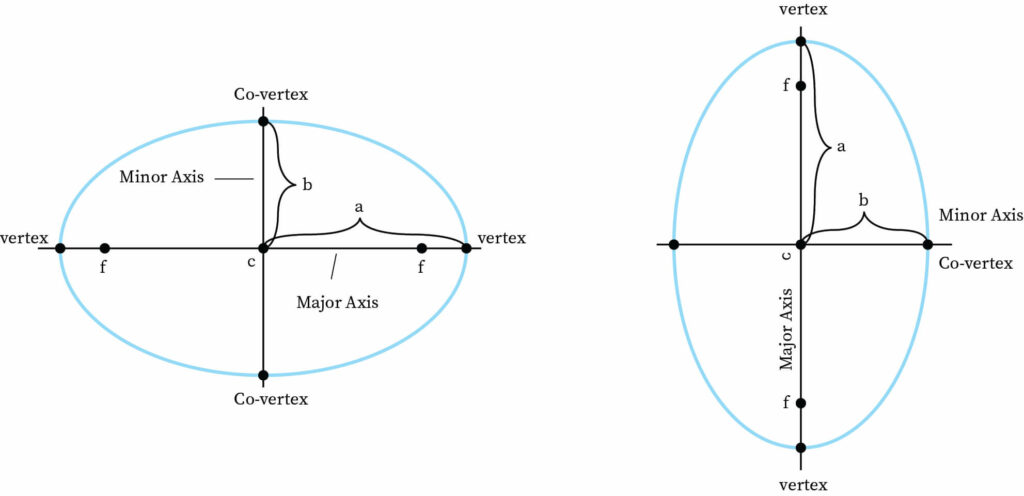
The major and minor axes are the symmetry axes of an ellipse. The co-vertices are the endpoints of the minor axis.. The endpoint of the minor axis is called the co-vertices. The form of the equation of the ellipse where its major axis is passing through the x-axis and the center would be , where the points a > b where a is the semi major axis and b is the semi minor axis.
The equation of the ellipse where its major axis passes through the y axis and the center would be , where the point b > a. These two equations are the standard form equation.
The general equation when the horizontal major axis of the ellipse passes through the x-axis and the center satisfying the condition a2> b2 would be:
This is horizontal ellipse.
The general equation when the vertical major axis of the ellipse passes through the y- axes and the center satisfying the condition b2 > a2 would be:
where these equations are ellipse centered at (h,k ), where c is the central distance from the center of the focus points. This equation describes the vertical ellipse. These are the equation of an ellipse.
The ratio of the distances from the center of the ellipse to one of its foci and to one of the vertices of the ellipse is called the eccentricity of an elliptical orbit. Its mathematical equation is where e is the eccentricity, c is the distance of the focus from the center and a is a point on the x-axis
The ellipse is symmetrical to both the coordinates and the x,y-axis where is a point on the elliptical curve, then are also points on the elliptical curve on its graph. The two vertices that lies on the major axis has a coefficient x2 which is its x coefficient and its y coefficient on the y-axis is y2
Latus rectum: The latus rectum is a line segment that is perpendicular to the major axis through any of the foci points and whose end points lie on the ellipse.
Let there be two points a and b be a foci of an ellipse , the locus of point P and for the constant c, ap+bp=c be the standard equation of the ellipse. The y intercept would be greater than 2ab. This ellipse is centered at the origin (0,0), the eccentricity e and the semi major axis a are in the x axis, then the foci are at and its directrix is .
Hyperbola and Ellipse Differentiation
In the study of Conics geometry, a hyperbola is a conic section formed when the right circular cone intersects the plane at an angle where both halves of the cones are intersected. This intersection gives two unbounded curve which are of mirror images of each other. Ellipse is very similar to hyperbola but the only difference is that an ellipse is defined as the sum of two distances from the foci of the points where a hyperbola is defined as the differences of the two distances. The similarity is that both have two axes of symmetry. The major and minor axis are also named transverse and conjugate axis in the study of conic sections.
Example
Let us take an example to understand the ellipse. The question follows as : Sketch the graph and find the vertices, end points of the minor axis and foci point for the equation .
So first convert the given equation to its standard form for the ellipse. To do that, divide the entire equation by the largest value in the denominator, here it is 16. so the standard form equation becomes. Since the largest value is 16, which is equal to a2 then 4 which is equal to b2, the ellipse has a horizontal major axis. So the values are a=4, b=2. Apply the formula to find the value of the y-intercept c= sqrt(16-4)=3.5 where the center is at (0,0). So the vertices are (4,0) and (-4, 0). Co-vertices: (0,2) and (0,-2) and foci are (3.5,0) and (-3.5,0). Hence the graph of the ellip2se can be constructed.
Context and Applications
This concept is studied in standards 10th, 11th and 12th as well as in Bachelors in Science (Physics and Mathematics)
Practice Problems
1) Determine the major axis and the length for the given equation of the ellipse:
Answer (1):
Step 1) Determine the major axis.
The standard equation of an ellipse with center is given by .
If , the major axis of the ellipse is parallel to the -axis of the coordinate system and if , the major axis is parallel to the -axis.
If , the length of the major axis is given by and if , the length of the major axis is given by .
Since 16 and 25 are the squares of 4 and 5 respectively, the given equation can be rewritten as .
Compare with standard equation of an ellipse to determine that and .
Because , the major axis is parallel to the -axis and its length is given by .
Step 2) Calculate the length of the major axis.
Multiply 5 by 2 to obtain the length of the major axis.
Hence, the major axis is parallel to the -axis and its length is 10 units.
2) Find the equation of the ellipse whose foci are at (0, -5 ) and (0, 5) and the length of its major axis is 14.
Answer (2):
Step 1) Determine the major axis.
The standard equation of an ellipse with center is given by .
If , the major axis of the ellipse is parallel to the -axis of the coordinate system and if , the major axis is parallel to the -axis.
If , the length of the major axis is given by and if , the length of the major axis is given by .
The foci of the required ellipse lie on the -axis which means that major axis of the required ellipse is parallel to the -axis.
Step 2) Calculate the length of the semi-major axis.
Because the major axis of the ellipse is parallel to the -axis, the length of the major axis is given by .
The given problem states that the length of the major axis is 14.
Set up the equation and then solve for .
Step 3) Calculate the length of the semi-minor axis.
The foci of an ellipse parallel to the -axis is given by and .
Compare and with and to determine that .
The formula to calculate the foci of an ellipse is given by .
Substitute and in and then solve for to obtain the length of the semi-minor axis.
Step 4) Substitute the lengths of the semi-major and semi-minor axis in the standard equation of an ellipse.
Substitute and in to obtain the equation of the ellipse.
Hence, the equation of the required ellipse is .
3) An ellipse has the following equation in its non stand form:
a) Find the equation of part of the graph of the given ellipse which is to the left of the y axis.
b) Determine the equation of the part of the graph of the ellipse that lies below the x-axis.
Answer 3(a):
Step 1) Rewrite the given equation in the standard form.
The standard equation of an ellipse with center is given by .
Divide both sides of the equation by 0.6 to obtain the standard from of the ellipse.
Step 2) Calculate the lengths of the semi-major and semi-minor axes.
Compare with standard equation of an ellipse to determine that and .
The equations and implies that the semi-major and semi-minor axis lengths are and .
The coordinate of vertices and co-vertices of the given ellipse are, therefore, and respectively.
Step 3) Calculate the foci of the ellipse.
The foci of an ellipse parallel to the -axis is given by and .
The formula to calculate the foci of an ellipse is given by .
Substitute and in to calculate the value of .
The foci of the given ellipse is .
Step 4) Use the vertices, co-vertices and foci to graph the function.
Use the points , , and to graph the given ellipse to the left of the -axis.
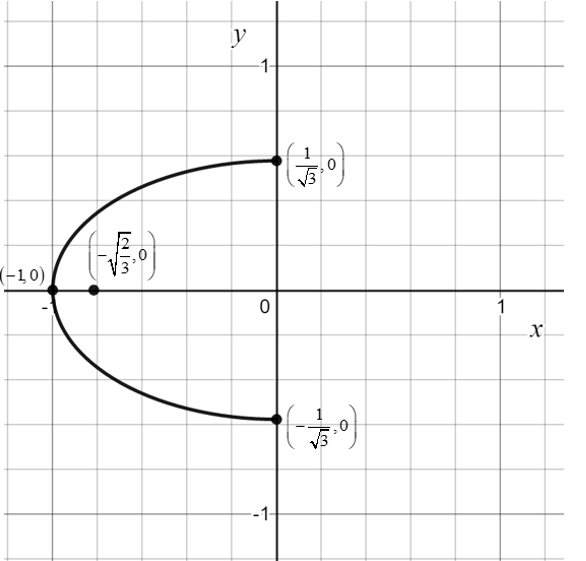
Answer 3(b):
Step 1) Use the vertices, co-vertices and foci of the ellipse to graph the function.
Use the points , , , and to graph of the ellipse that lies below the -axis.
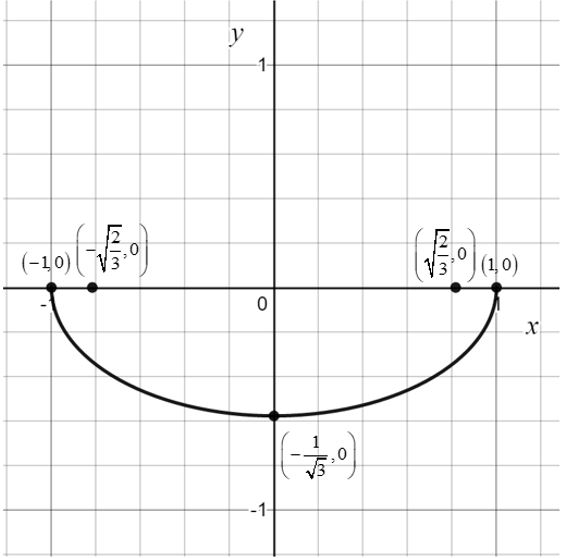
Want more help with your geometry homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Vertices Of An Ellipse Homework Questions from Fellow Students
Browse our recently answered Vertices Of An Ellipse homework questions.