What mass of iron (III) sulfate is present in 100 cm3 of the solution used to measure the standard electrode potential of this cell? A cell could be set up as shown to measure the electrode potential for the reactionbetween iron(II) sulfate and chromium(Il) sulfate:Fe"(aq) + Cr (aq) Fe (aq) + Cr* (aq)salt bridgeVplatinum electrodeplatinum electrodeFe (aq) / Fe"(aq)Cr* (aq) / Cr* (aq)

Answered: What mass of iron (III) sulfate is…

What mass of iron (III) sulfate is present in 100 cm3 of the solution used to measure the standard electrode potential of this cell

Principles of Modern Chemistry

8th Edition

ISBN:9781305079113

Author:David W. Oxtoby, H. Pat Gillis, Laurie J. Butler

Publisher:David W. Oxtoby, H. Pat Gillis, Laurie J. Butler

Chapter17: Electrochemistry

Section: Chapter Questions

Problem 76AP

See similar textbooks

Related questions

Q: Why is it necessary to use the standard hydrogen half-cell as a reference when calculating standard…

A: Given statement is : Why is it necessary to use the standard hydrogen half-cell as a reference when…

Q: >Why do some electrochemical cells employ inert electrodes such as platinum?

A: In some redox reactions, may be one of the reactant or product and sometimes both reactant and…

Q: The standard reduction potential of the Pb2+/Pb electrode is -0.13 V and the standard cell potential…

Q: Determine the cell potential of the following system: a) Pb/PbSO4//Pb2+/Pb

Q: The standard potential of a Daniell cell, with cell reaction Zn(s) + Cu2+(aq) → Zn2+(aq) + Cu(s), is…

A: The reaction:

Q: The table below gives the standard electrode potential values of some electrode. What standard…

A: The potential of all electrodes are measured by comparing their potential to that of standard…

Q: Explain the significance of the standard hydrogen electrode (SHE) in the tabulation of standard…

A: The standard hydrogen electrode (SHE) in the tabulation of standard reduction potentials refers to…

Q: Calculate the standard free-energy change at 298K for the zinc-copper voltaic cell, which has a…

Q: Devise cells in which the following are the reactions and calculate the standard cell potential in…

A: An Electrochemical is made of cathode and anode. In the cell process goes on are: oxidation and…

Q: Which reference electrode is used to measure the electrode potential of other electrodes?

A: A reference electrode is an electrode which has a stable and well known electrode potential.

Q: Calculate the cell potential for the galvanic cell in w

Q: How is equilibrium constant of a reaction related to standard cell potential?

A: How is equilibrium constant of a reaction related to standard cell potential?

Q: Tabulated thermodynamic data can be used to predict the standard potential of a cell even if it…

A: Given: The balanced equation of the reaction is given as, Standard Gibbs energy of the reaction =…

Q: Consider the following reaction at 298K. Hg2+ (aq) + Zn(s)→→→→→→ Hg({) + Zn²+ (aq) The standard…

A: The equation ∆G∘ = -nFE∘Cell can also be used to calculate the potential of half-cell by addition or…

Q: The standard cell potential for the Daniell cell, Zn(s) + Cu2+(aq) → Zn2+(aq) + Cu(s) is +1.102 V at…

Q: Why is it not possible to measure single electrode potential?

A: Potential difference in the electro-chemical cell is generated due to the redox reaction occurring…

Q: What is the standard cell potential of a galvanic cell represented by the reaction below? Mg + Sn2+…

Q: Describe the standard hydrogen electrode (SHE) and explain its use in determining standard electrode…

A: For a half-cell, we cannot measure the potential directly. We can only measure the overall potential…

Q: A fuel cell is constructed in which both electrodes make use of the oxidation of methane. The…

A: (a)

Q: Fe (s) + O2(g) + 2H2O (l) → Fe3+ + 4OH- Balance the simple redox reaction, If the standard change…

A: Oxidation is the loss of electrons and reduction is the gain of electrons.

Q: For the standard cell potentials given here, determine the ΔG° for the cell in kJ.(a) 0.000 V, n =…

Q: In an experiment of a redox reaction, an electrochemical cell has been set up by connecting a vessel…

A: The balanced redox reaction that represents the described galvanic cell can be written as follows:…

Q: What does a negative standard cell potential imply about the reaction?

A: The potential difference between the cathode and anode half cell under the standard conditions of…

Q: Explain Standard Electrode Potentials?

A: If the temperature is 298 K and the pressure is 1 atm,then these are known to be the standard…

Q: For the reaction; 4H+ + PbO2 + 2 Fe 2+ → 2 Fe 3+ + Pb2+ + 2 H2O, the standard electrode…

Q: For the following redox reaction calculate the standard cell potential of the reaction. Redox…

A: We should know the oxidation reaction and the reduction reaction. In Oxidation reaction we have loss…

Q: How are standard electrode potentials measured?

A: Standard electrode potential is referred to Eo of a cell and is in an electrochemical cell at a…

Q: Calculate the actual cell potential if you have a 1 M solution of MgSO4, but only a 0.5 M solution…

Q: A nonstandard cell is made by replacing the 1.0 M solutions of Cu(NO3)2 and Sn(NO3)2 in the standard…

A: Answer: 1. Let the standard electrode potential 1 M solution of Cu(NO3)2 and Sn(NO3)2 be E0 So,…

Q: A current of 0.452 Amps is passed through an electrolytic cell containing molten CaCl2 for 1.50 hrs.…

Q: 1. (a) Balance the following simple redox reaction. Fe (s) + O₂(g) + 2H₂O (1)→ Fe³+ + 4 OH (b) If…

Q: Devise cells in which the following are the reactions and calculate the standard cell potential in…

Q: Tabulated thermodynamic data can be used to predict the standard potential of a cell even if it…

A: Given: The balanced equation of the reaction is given as, Standard Gibbs energy of the reaction =…

Q: The equilibrium constant of a cell with a cell potential of 0 V is a. 1.5 b. 2.5 c. 0 d. 1 e. 0.5 f.…

A: To Solve this problem we will calculate the equilibrium constant .

Q: = standard potential of the cell, E°cell?

Q: 4H* + 4e + O2 -> 2 H2O, E• = + 0.82 V NAD* + H* + 2e -> NADH, E• = -0.32 V applied to the…

Q: Given that the standard cell potential is 0.019 V and the overall equation is 2 Cr³⁺ (aq) + 3 Zn (s)…

A: The Nernst equation is shown below,

Q: What do you mean by ( i) negative standard electrode potential and(ii) positive standard electrode…

A: Standard electrode potential is defined as the potential of the electrode at the standard conditions…

Q: Draw a galvanic cell consisting of a chromium and cobalt electrode and calculate the standard cell…

Q: Give the reason why it is necessary to use hydrogen as a standard to define the standard potential…

A: A standard electrode is an electrode used as a reference in electrochemical reactions and this…

Q: How long (in hours) must a current of 5.0 amperes be maintained to electroplate 60g of calcium from…

A: Given that, Weight of Moltan CaCl2 w = 60 g Current I = 5 A How much time of current maintained by…

Q: Calculate the cell potential for the galvanic cell (in volts) in which the following reaction occurs…

A: The given reaction is: Reduction potential values are as follows: Since Ti is getting oxidized to…

Q: In electroplating operation, the cell potential is sometimes 0V. Why is zero potential possible in…

A: Electroplating is the process of coating metal using an electric current. This is mainly for the…

Q: Balance the following reaction. Calculate the cell potential and Gibbs free energy of this reaction…

A: The balanced redox reaction can be written as: MnO4- + 8H+ + 5e- → Mn2+ + 4H2O (Reduction)5Ce3+ →…

Q: What is the value of the standard copper potential in half-cell reactions?

A: Solution- standards copper potential in half-cell - Ca2++2e− ⟶ Ca −2.868

Question

What mass of iron (III) sulfate is present in 100 cm3 of the solution used to measure the standard electrode potential of this cell?

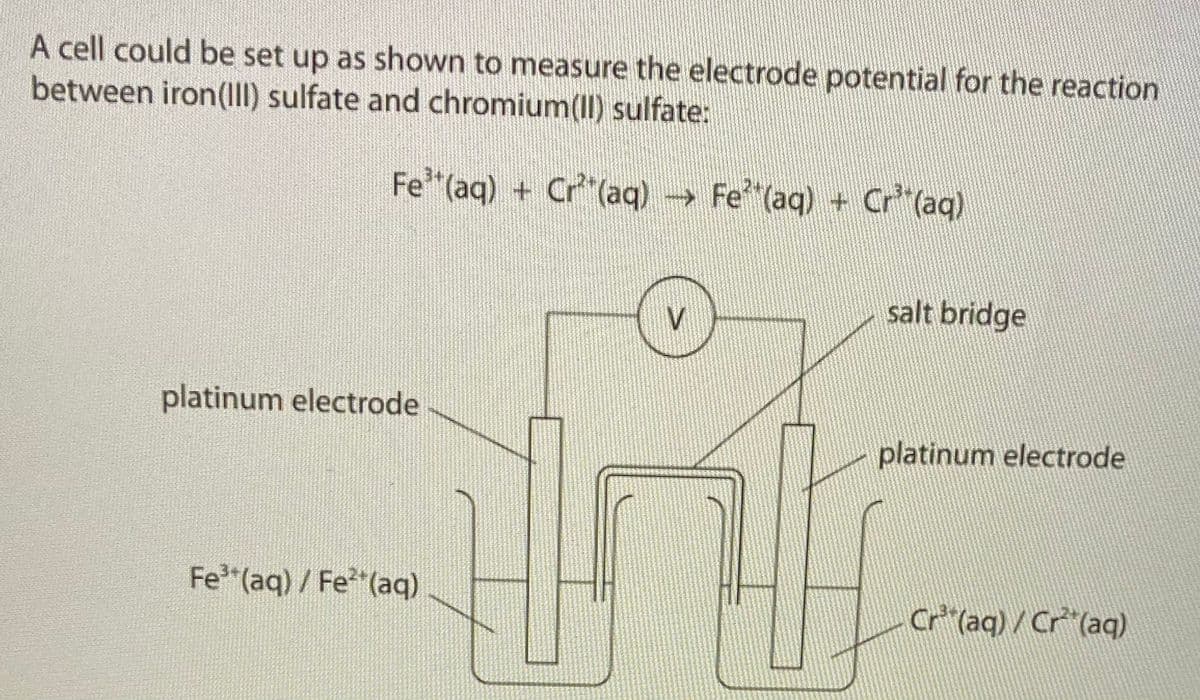
A cell could be set up as shown to measure the electrode potential for the reaction
between iron(II) sulfate and chromium(Il) sulfate:
Fe"(aq) + Cr (aq) Fe (aq) + Cr* (aq)
salt bridge
V
platinum electrode
platinum electrode
Fe (aq) / Fe"(aq)
Cr* (aq) / Cr* (aq)

Expert Solution

This question has been solved!

Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.

This is a popular solution!

SEE SOLUTION Check out a sample Q&A here

Step 1

VIEW

Step 2

VIEW

Trending now

This is a popular solution!

Step by step

Solved in 2 steps

SEE SOLUTION Check out a sample Q&A here

Knowledge Booster

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, chemistry and related others by exploring similar questions and additional content below.

Similar questions

In another experiment, Fischl used chromium metal to form an electrode she can use for her voltaic cell. She wanted to determine the electric potential produced by the chromium electrode (and 1.0 M of its corresponding electrolyte solution) with a Copper electrode in 0.10 M CuSO4 solution at 25 oC. Predict the following: OHR and RHR Number of electrons involved in the redox reaction Overall reaction for the voltaic cell Standard cell potential, Eocell Theoretical Ecell If the measured Ecell was 0.75 V, calculate the percent error. Oz suggested that they increase the concentration of CuSO4 solution used. What will be the effect on the measured potential?
In a historical industrial process Co(CO)4H is generated in-situ from CoI2, CO and H2O. By-products are CO2 and HI. Give the two relevant half-equations and then construct the full redox equation.
You are in the field measuring redox potentials of wetland soils using a Pt and saturated calomel electrodes. Your potentiometer reads -0.100 V. What is the actual Eh?
The standard potential of the cell calomel || nonesuch composed of a calomel electrode and a nonesuch electrode is -1978 mV at 25oC. Find the standard potential of the nonesuch electrode at 25oC.[-1.710] The answer is enclosed in the bracket, I would like to know how it was obtained. Thank you!
It is desired to assemble a concentration cell with a potential of 120 mV withtwo Zn(s) electrodes immersed, each one, in a ZnSO4 solution. What should be theratio between Zn2+ activities in the two electrodes to reach the desired potential?
An aqueous copper (II) chloride solution is electrolyzed for a period of 156 minutes. Using a current of 9.00 A. If inert electrodes are used in the process, how many grams of copper were removed from the solution?
a) Given the redox reaction equation below: MnO4 - (aq) + Zn (s) → Mn2+ (aq) + Zn2+ (aq) i. Complete and balance the above equation in acidic solution. ii. Calculate the standard potential produced from the above redox reaction. iii. Write the Qc expression for the above reaction
Black-and-white photographic film is coated with silver halides. Because silver is expensive, the manufacturer monitors the Ag+ content of the waste stream, [Ag+]waste, from the plant with an Ag+-selective electrode at 25oC. A stream of known Ag+ concentration, [Ag+]standard, is passed over the electrode in turn with the waste stream and the data recorded by a computer. (a) Write the equations relating the nonstandard cell potential to the standard cell potential and [Ag+] for each solution. (b) Combine these into a single equation to find [Ag+]waste. (c) Rewrite the equation from part (b) to find [Ag+]waste in ng/L. (d) If Ewaste is 0.003 V higher than Estandard, and the standard solution contains 1000. ng/L, what is [Ag+]waste? (e) Rewrite the equation from part (b) to find [Ag+]waste for a system in which T changes and Twaste and Tstandard may be different.
Purification of chromium can be achieved by electrorefining chromium from an impure chromium anode onto a pure chromium cathode in an electrolytic cell. How many hours will it take to plate 10.5 kg of chromium onto the cathode if the current passed through the cell is held constant at 35.0 A? Assume the chromium in the electrolytic solution is present as Cr3+. time:_____ h
Black-and-white photographic film is coated with silver halides. Because silver is expensive, the manufacturer monitors the Ag⁺ content of the waste stream, [Ag⁺]ᵥᵥₐₛₜₑ, from the plantwith an Ag-selective electrode at 25°C. A stream of known Ag⁺ concentration, [Ag⁺](standard), is passed over the electrode inturn with the waste stream and the data recorded by a computer.(a) Write the equations relating the nonstandard cell potential tothe standard cell potential and [Ag⁺] for each solution.(b) Combine these into a single equation to find [Ag⁺]ᵥᵥₐₛₜₑ.(c) Rewrite the equation from part (b) to find [Ag⁺]ᵥᵥₐₛₜₑ in ng/L.(d) If Eᵥᵥₐₛₜₑ is 0.003 V higher than E(standard), and the standard so-lution contains 1000. ng/L, what is [Ag⁺]ᵥᵥₐₛₜₑ?(e) Rewrite the equation in part (b) to find [Ag⁺]ᵥᵥₐₛₜₑ for a sys-tem in which T changes and Tᵥᵥₐₛₜₑ and T(standard) may be different.
The exchange current density at the electrode Pt| Fe3+| Fe2+ is 2.4 x 10-3 A cm-2, How many electrons are transported through the double layer per second in the cell (area of 1 cm2 each)? Estimate the number of times per second that a single atom on the surface takes part in an electron transfer event, assuming that the atom occupies 280 pm2 of the surface of the electrode
2V is applied across an electrolytic cell containing 1.0M NaNO3. What reaction occurs at the anode? Show your work What reaction occurs at the cathode? Show your work Diagram the cell (assume the two electrodes are in 1 beaker). How many minutes does it take to form 10.0L of your anodic product measured at 99.8kPa and 28oC if a current of 1.3A is passed through the electrolytic cell?