1.50 kg 0.300 m 5.00 m/s 2.60 kg Show your work in detail) Starting with an initial speed of 5.00 m/s at a height of 0.300 m, a 1.50-kg ball swings downward and strikes a 2.60-kg ball that is at rest, as the drawing shows. Find the speed of the 1.50-kg ball just before impact. 4. Assuming that the collision is completely inelastic (two b. balls stuck together), find the velocities (magnitude and direction) of both balls just after the collision. How high does balls together swing after the collision, C. ignoring air resistance?
1.50 kg 0.300 m 5.00 m/s 2.60 kg Show your work in detail) Starting with an initial speed of 5.00 m/s at a height of 0.300 m, a 1.50-kg ball swings downward and strikes a 2.60-kg ball that is at rest, as the drawing shows. Find the speed of the 1.50-kg ball just before impact. 4. Assuming that the collision is completely inelastic (two b. balls stuck together), find the velocities (magnitude and direction) of both balls just after the collision. How high does balls together swing after the collision, C. ignoring air resistance?
Classical Dynamics of Particles and Systems
5th Edition
ISBN:9780534408961
Author:Stephen T. Thornton, Jerry B. Marion
Publisher:Stephen T. Thornton, Jerry B. Marion
Chapter9: Dynamics Of A System Of Particles
Section: Chapter Questions
Problem 9.34P
Related questions
Topic Video
Question
100%
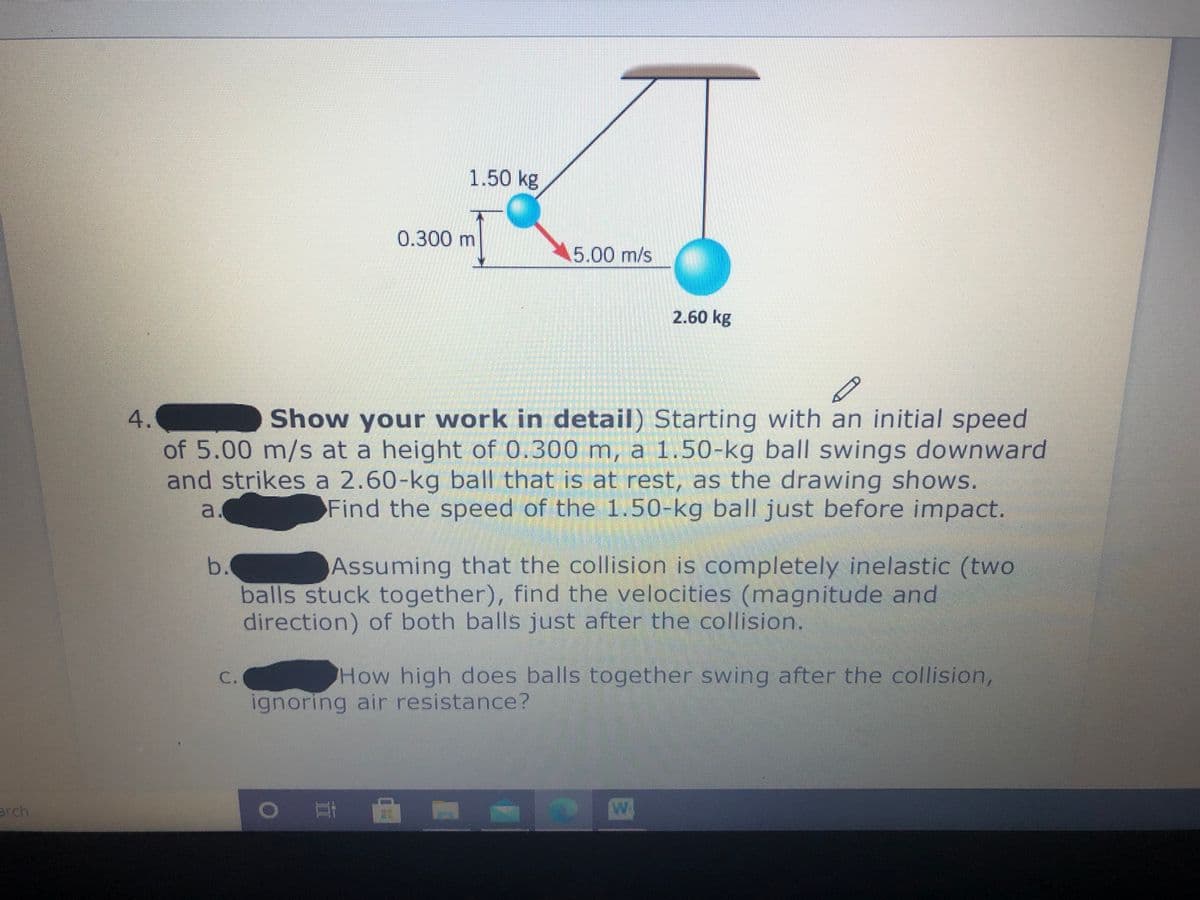
Transcribed Image Text:1.50 kg
0.300 m
5.00 m/s
2.60 kg
Show your work in detail) Starting with an initial speed
of 5.00 m/s at a height of 0.300 m, a 1.50-kg ball swings downward
and strikes a 2.60-kg ball that is at rest, as the drawing shows.
Find the speed of the 1.50-kg ball just before impact.
4.
a.
Assuming that the collision is completely inelastic (two
b.
balls stuck together), find the velocities (magnitude and
direction) of both balls just after the collision.
C.
How high does balls together swing after the collision,
ignoring air resistance?
arch
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Recommended textbooks for you

Classical Dynamics of Particles and Systems
Physics
ISBN:
9780534408961
Author:
Stephen T. Thornton, Jerry B. Marion
Publisher:
Cengage Learning

College Physics
Physics
ISBN:
9781305952300
Author:
Raymond A. Serway, Chris Vuille
Publisher:
Cengage Learning

Physics for Scientists and Engineers: Foundations…
Physics
ISBN:
9781133939146
Author:
Katz, Debora M.
Publisher:
Cengage Learning

Classical Dynamics of Particles and Systems
Physics
ISBN:
9780534408961
Author:
Stephen T. Thornton, Jerry B. Marion
Publisher:
Cengage Learning

College Physics
Physics
ISBN:
9781305952300
Author:
Raymond A. Serway, Chris Vuille
Publisher:
Cengage Learning

Physics for Scientists and Engineers: Foundations…
Physics
ISBN:
9781133939146
Author:
Katz, Debora M.
Publisher:
Cengage Learning

University Physics Volume 1
Physics
ISBN:
9781938168277
Author:
William Moebs, Samuel J. Ling, Jeff Sanny
Publisher:
OpenStax - Rice University


College Physics
Physics
ISBN:
9781285737027
Author:
Raymond A. Serway, Chris Vuille
Publisher:
Cengage Learning