10.22 A political scientist is studying the impact of a political debate between candidates for governor in a small western state. The scientist wants to evaluate the proportion of registered votes who switch their preference after viewing the debate. The following table contain the data from 75 registered voters. Preference After Debate Preference Before Debate CandidateA Candidate B Candidate A Candidate B 13 28 28 a. Test whether there was a shift away from candidate A after the debate. Use a .05 Carefully state your conclusion. b. Construct a 95% confidence interval for the change after the debate in the proportion of registered voters preferring candidate A
10.22 A political scientist is studying the impact of a political debate between candidates for governor in a small western state. The scientist wants to evaluate the proportion of registered votes who switch their preference after viewing the debate. The following table contain the data from 75 registered voters. Preference After Debate Preference Before Debate CandidateA Candidate B Candidate A Candidate B 13 28 28 a. Test whether there was a shift away from candidate A after the debate. Use a .05 Carefully state your conclusion. b. Construct a 95% confidence interval for the change after the debate in the proportion of registered voters preferring candidate A
MATLAB: An Introduction with Applications
6th Edition
ISBN:9781119256830
Author:Amos Gilat
Publisher:Amos Gilat
Chapter1: Starting With Matlab
Section: Chapter Questions
Problem 1P
Related questions
Question
100%
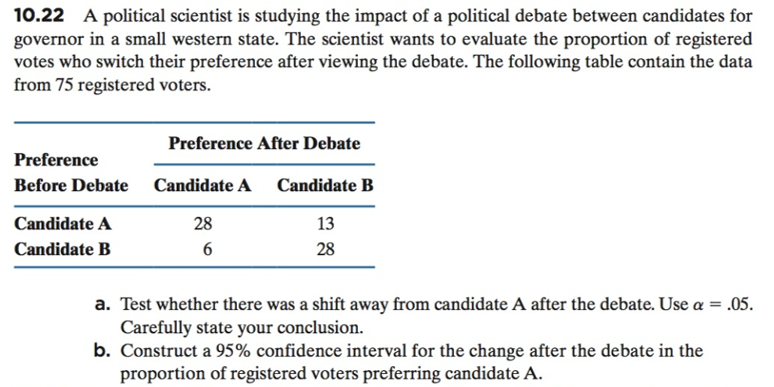
Transcribed Image Text:10.22 A political scientist is studying the impact of a political debate between candidates for
governor in a small western state. The scientist wants to evaluate the proportion of registered
votes who switch their preference after viewing the debate. The following table contain the data
from 75 registered voters.
Preference After Debate
Preference
Before Debate
CandidateA
Candidate B
Candidate A
Candidate B
13
28
28
a. Test whether there was a shift away from candidate A after the debate. Use a .05
Carefully state your conclusion.
b. Construct a 95% confidence interval for the change after the debate in the
proportion of registered voters preferring candidate A
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 1 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
A political scientist is studying the impact of a political debate between candidates for governor in a small western state. The scientist wants to evaluate the proportion of registered voters who switched their preference after viewing the debate. The following table contain the data from 75 registered voters:
Construct a 95% confidence interval for the change after the debate in the proportion of registered voters preferring candidate A.
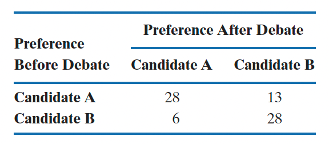
Transcribed Image Text:Preference
Before Debate
Candidate A
Candidate B
Preference After Debate
Candidate A
28
6
Candidate B
13
28
Solution
Recommended textbooks for you

MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc

Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning

MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc

Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning

Elementary Statistics: Picturing the World (7th E…
Statistics
ISBN:
9780134683416
Author:
Ron Larson, Betsy Farber
Publisher:
PEARSON

The Basic Practice of Statistics
Statistics
ISBN:
9781319042578
Author:
David S. Moore, William I. Notz, Michael A. Fligner
Publisher:
W. H. Freeman

Introduction to the Practice of Statistics
Statistics
ISBN:
9781319013387
Author:
David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:
W. H. Freeman