Chapter 15, Problem 039 The balance wheel of a watch oscillates with angular amplitude 0.64n rad and period 0.68 s. Find (a) the maximum angular speed of the wheel, (b) the angular speed of the wheel at displacement 0.64n/2 rad, and (c) the magnitude of the angular acceleration at displacement 0.64n,/4 rad. (a) Number Units (b) Number Units (c) Number Units
Chapter 15, Problem 039 The balance wheel of a watch oscillates with angular amplitude 0.64n rad and period 0.68 s. Find (a) the maximum angular speed of the wheel, (b) the angular speed of the wheel at displacement 0.64n/2 rad, and (c) the magnitude of the angular acceleration at displacement 0.64n,/4 rad. (a) Number Units (b) Number Units (c) Number Units
Physics for Scientists and Engineers: Foundations and Connections
1st Edition
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Katz, Debora M.
Chapter16: Oscillations
Section: Chapter Questions
Problem 9PQ: A simple harmonic oscillator has amplitude A and period T. Find the minimum time required for its...
Related questions
Question
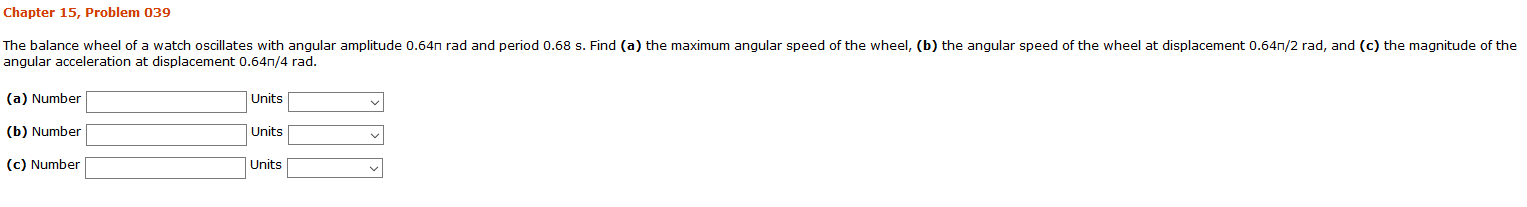
Transcribed Image Text:Chapter 15, Problem 039
The balance wheel of a watch oscillates with angular amplitude 0.64n rad and period 0.68 s. Find (a) the maximum angular speed of the wheel, (b) the angular speed of the wheel at displacement 0.64n/2 rad, and (c) the magnitude of the
angular acceleration at displacement 0.64n,/4 rad.
(a) Number
Units
(b) Number
Units
(c) Number
Units
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 4 steps with 3 images

Recommended textbooks for you

Physics for Scientists and Engineers: Foundations…
Physics
ISBN:
9781133939146
Author:
Katz, Debora M.
Publisher:
Cengage Learning

Physics for Scientists and Engineers
Physics
ISBN:
9781337553278
Author:
Raymond A. Serway, John W. Jewett
Publisher:
Cengage Learning

Physics for Scientists and Engineers with Modern …
Physics
ISBN:
9781337553292
Author:
Raymond A. Serway, John W. Jewett
Publisher:
Cengage Learning

Physics for Scientists and Engineers: Foundations…
Physics
ISBN:
9781133939146
Author:
Katz, Debora M.
Publisher:
Cengage Learning

Physics for Scientists and Engineers
Physics
ISBN:
9781337553278
Author:
Raymond A. Serway, John W. Jewett
Publisher:
Cengage Learning

Physics for Scientists and Engineers with Modern …
Physics
ISBN:
9781337553292
Author:
Raymond A. Serway, John W. Jewett
Publisher:
Cengage Learning

Principles of Physics: A Calculus-Based Text
Physics
ISBN:
9781133104261
Author:
Raymond A. Serway, John W. Jewett
Publisher:
Cengage Learning

Physics for Scientists and Engineers, Technology …
Physics
ISBN:
9781305116399
Author:
Raymond A. Serway, John W. Jewett
Publisher:
Cengage Learning

Classical Dynamics of Particles and Systems
Physics
ISBN:
9780534408961
Author:
Stephen T. Thornton, Jerry B. Marion
Publisher:
Cengage Learning