Chapter 22, Problem 024 Your answer is partially correct. Try again. A thin nonconducting rod with a uniform distribution of positive charge Q is bent into a circle of radius R (see the figure). The central perpendicular axis through the ring is a z axis, with the origin at the center of the ring. what is the magnitude of the electric field due to the rod at (a)2-0 and (b)2 = oo? (c) In terms of R, at what positive value ofz is that magnitude maximum? (d) If R = 2.30 cm and Q = 4.05 pC, what is the maximum magnitude? (a) NumberTo Units N/C or V/m UnitsT N/C or V/m Units No units 1 Units N/C or V/m (b) Numbe (c) Number (d) Number
Chapter 22, Problem 024 Your answer is partially correct. Try again. A thin nonconducting rod with a uniform distribution of positive charge Q is bent into a circle of radius R (see the figure). The central perpendicular axis through the ring is a z axis, with the origin at the center of the ring. what is the magnitude of the electric field due to the rod at (a)2-0 and (b)2 = oo? (c) In terms of R, at what positive value ofz is that magnitude maximum? (d) If R = 2.30 cm and Q = 4.05 pC, what is the maximum magnitude? (a) NumberTo Units N/C or V/m UnitsT N/C or V/m Units No units 1 Units N/C or V/m (b) Numbe (c) Number (d) Number
Principles of Physics: A Calculus-Based Text
5th Edition
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Raymond A. Serway, John W. Jewett
Chapter19: Electric Forces And Electric Fields
Section: Chapter Questions
Problem 73P: Two infinite, nonconducting sheets of charge are parallel to each other as shown in Figure P19.73....
Related questions
Question
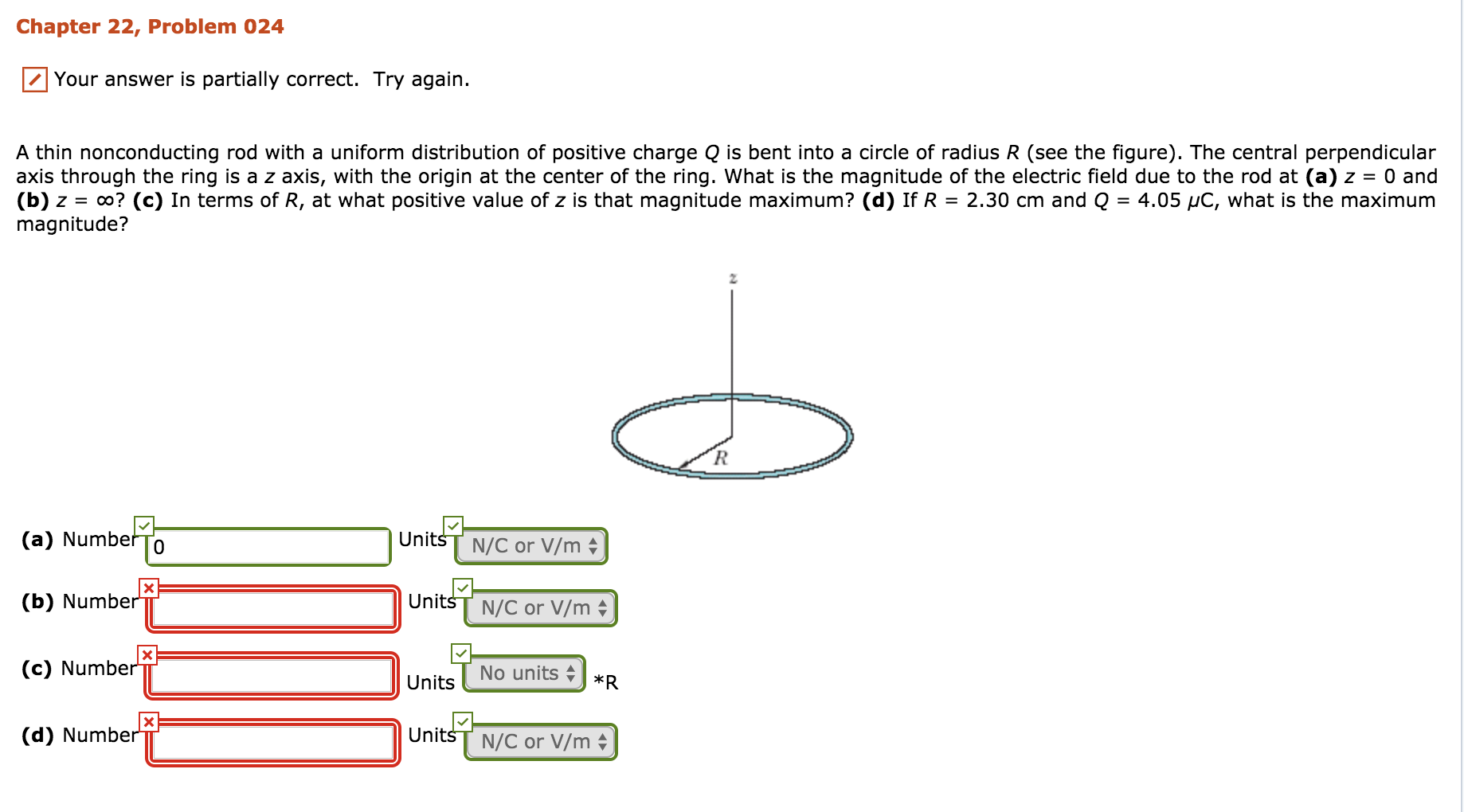
Transcribed Image Text:Chapter 22, Problem 024
Your answer is partially correct. Try again.
A thin nonconducting rod with a uniform distribution of positive charge Q is bent into a circle of radius R (see the figure). The central perpendicular
axis through the ring is a z axis, with the origin at the center of the ring. what is the magnitude of the electric field due to the rod at (a)2-0 and
(b)2 = oo? (c) In terms of R, at what positive value ofz is that magnitude maximum? (d) If R = 2.30 cm and Q = 4.05 pC, what is the maximum
magnitude?
(a) NumberTo
Units N/C or V/m
UnitsT N/C or V/m
Units No units 1
Units N/C or V/m
(b) Numbe
(c) Number
(d) Number
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 4 steps with 3 images

Recommended textbooks for you

Principles of Physics: A Calculus-Based Text
Physics
ISBN:
9781133104261
Author:
Raymond A. Serway, John W. Jewett
Publisher:
Cengage Learning

Physics for Scientists and Engineers: Foundations…
Physics
ISBN:
9781133939146
Author:
Katz, Debora M.
Publisher:
Cengage Learning

Principles of Physics: A Calculus-Based Text
Physics
ISBN:
9781133104261
Author:
Raymond A. Serway, John W. Jewett
Publisher:
Cengage Learning

Physics for Scientists and Engineers: Foundations…
Physics
ISBN:
9781133939146
Author:
Katz, Debora M.
Publisher:
Cengage Learning