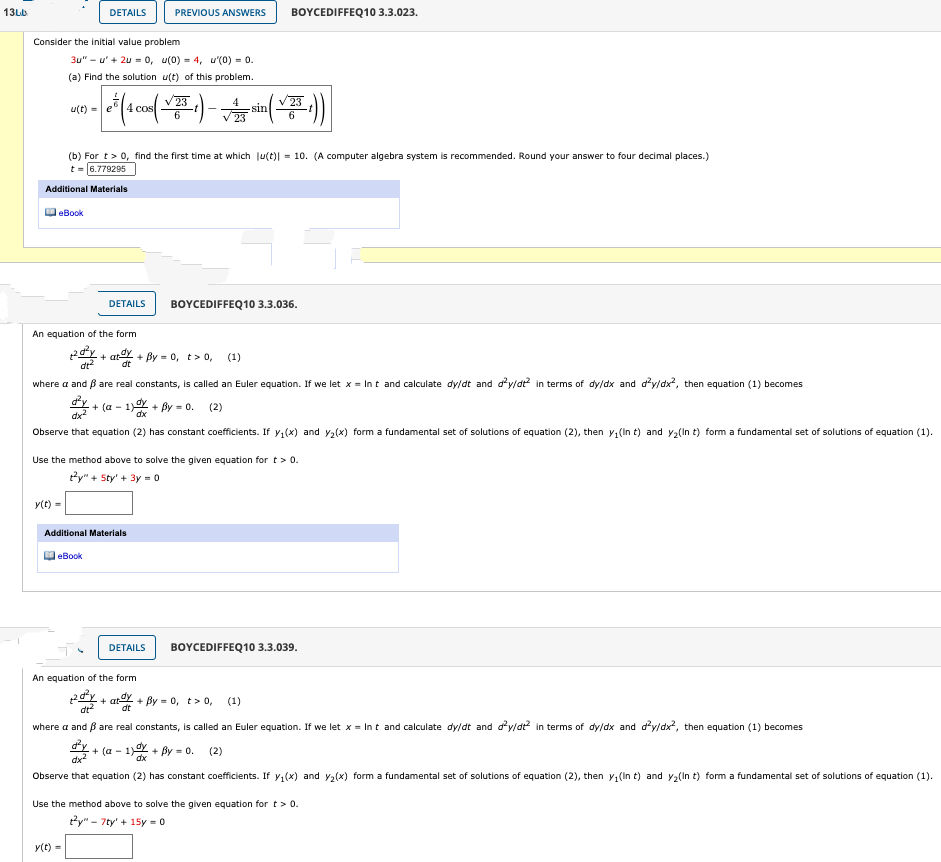
Lb DETAILS PREVIOUS ANSWERS BOYCEDİFFEQ10 3.3.023. Consider the initial value problem 3u" - u' + 2u - 0, u(0) - 4, u'(0) - 0. (a) Find the solution u(t) of this problem. 23 u(t) - (b) For t> 0, find the first time at which Ju(t)| - 10. (A computer algebra system is recommended. Round your answer to four decimal places.) t-6.779295 Additional Materials DeBook DETAILS BOYCEDIFFEQ10 3.3.036. An equation of the form + at + By - 0, t> 0, (1) dt where a and B are real constants, is called an Euler equation. If we let x = Int and calculate dy/dt and dy/dt in terms of dy/dx and dy/dx, then equation (1) becomes dy + (a - 1) + By = 0. dx (2) dx Observe that equation (2) has constant coefficients. If y,(x) and y2(x) form a fundamental set of solutions of equation (2), then y,(In t) and y2(in t) form a fundamental set of solutions of equation (1). Use the method above to solve the given equation for t > 0. By" + Sty' + 3y = 0 y(t) = Additional Materials DeBook DETAILS BOYCEDIFFEQ10 3.3.039. An equation of the form dy + atdy + By - 0, t> 0, (1) dr where a and ß are real constants, is called an Euler equation. If we let x = Int and calculate dy/dt and dy/dt in terms of dy/dx and d'y/dx?, then equation (1) becomes + (a - 1 + By = 0. (2) dx dx Observe that equation (2) has constant coefficients. If y,(x) and y2(x) form a fundamental set of solutions of equation (2), then y,(In t) and y2(In t) form a fundamental set of solutions of equation (1). Use the method above to solve the given equation for t> 0. ty" - 7ty' + 15y - 0 y(t) =
Unitary Method
The word “unitary” comes from the word “unit”, which means a single and complete entity. In this method, we find the value of a unit product from the given number of products, and then we solve for the other number of products.
Speed, Time, and Distance
Imagine you and 3 of your friends are planning to go to the playground at 6 in the evening. Your house is one mile away from the playground and one of your friends named Jim must start at 5 pm to reach the playground by walk. The other two friends are 3 miles away.
Profit and Loss
The amount earned or lost on the sale of one or more items is referred to as the profit or loss on that item.
Units and Measurements
Measurements and comparisons are the foundation of science and engineering. We, therefore, need rules that tell us how things are measured and compared. For these measurements and comparisons, we perform certain experiments, and we will need the experiments to set up the devices.
Show your all calculation and solve all problems
Trending now
This is a popular solution!
Step by step
Solved in 4 steps with 5 images









