What are Speed, Time, and Distance?

Imagine you and 3 of your friends are planning to go to the playground at 6 in the evening. Your house is one mile away from the playground and one of your friends named Jim must start at 5 pm to reach the playground by walk. The other two friends are 3 miles away.

To reach the playground, it might take 10 minutes if you walk or 4 minutes if you go by cycle. So, it is enough if you start from home around 5:50 pm or 5:55 pm. But it is impossible for Jim to start at 5:50 pm and reach at 6 pm? Can you guess why? It is because it takes 1 hour for him to walk to the playground. He might be so many miles away. But he can reach early if he chooses to take a train or car.

Although all the 4 must reach by 6 pm, the time you start is different for everyone. The distance of the playground to the respective homes is different. The speed is different when you walk or go by train.

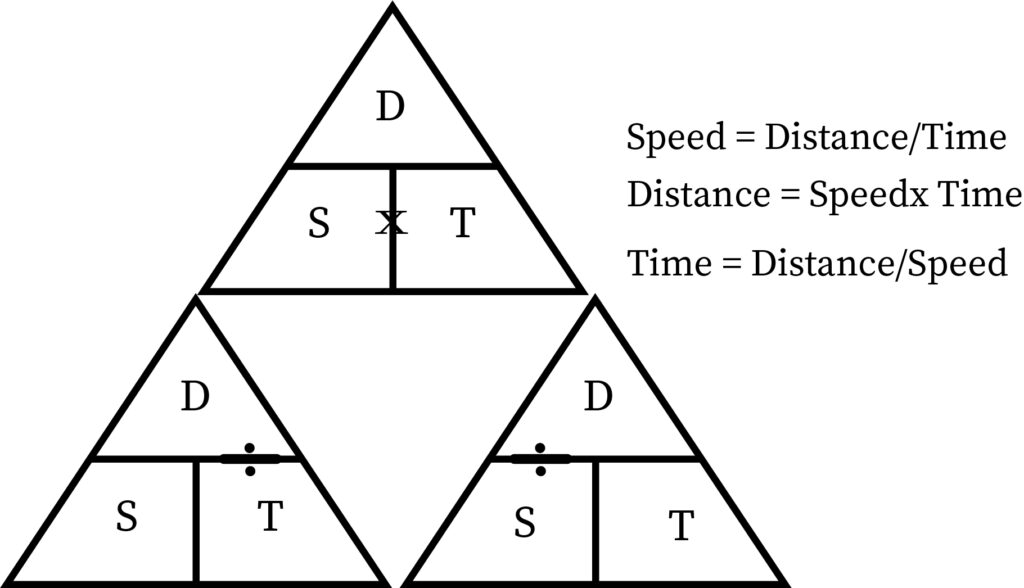
What is the Relationship between Speed, Time, and Distance?

Speed, time, and distance are interdependent terms.

Suppose that you are writing an exam which is conducted for three hours. If there are only 10 minutes left and you must write 2 more long questions, will you write slowly or will you increase your speed?

Here, speed and time are interdependent. In the same way, if you must go home soon after the exam, you must walk fast. So, speed and time are interdependent. If your home is very far and you must reach there in 10 minutes, then you must travel soon. Thus, speed, time, and distance are related to one another.

The speed of the body is the distance travelled by the body in unit time. As speed increases, the distance also increases. So, we can say, speed and distance are directly proportional to each other. It is mathematically represented as follows.

How does Speed affect Time and Distance?

As speed increases, the time required to cover the distance decreases.

So, speed and time are inversely proportional to each other. It is mathematically represented as follows.

The Formula for calculating Speed

The speed of an object can be calculated by taking the distance divided by time.

The unit of the speed is meter per second denoted as m/s or kilometer per hour denoted as km/hr.

Conversion of Units

The following formula is used for converting kilometer per hour to meters per second.

1km/hr =$\frac{5}{18}$m/s

In the same way, converting meter per second to kilometer per hour is given as follows.

1m/s=$\frac{18}{5}$km/hr

How to Solve Speed, Time, and Distance Problems?

Let us see an example.

A boat covers a distance of 750m in 4 minutes. Find the speed of the boat?

Solution:

Let us write the given information.

Distance =750 m

Time = 4 minutes

So, the speed is calculated as follows.

$\begin{array}{c}\text{speed=}\frac{\text{750}}{4}\\ =187.5m/\min \end{array}$

The speed of the boat is $187.5m/\min$.

The Formula for Calculating Distance  

The distance can be calculated by multiplying speed and time.

Units of distance are meters (m) or kilometers (km).

How to find the Distance when Speed and Time are Given?

A bike travels at speed of 40 km/hr. How much distance it will travel in 3 hours?

Solution:

Let us write the given information.

Speed =40kmph

Time = 3 hours

So, the distance is calculated as follows.

The distance travelled by bike is 120km.

The Formula for Calculating Time

The time can be calculated as the distance divided by speed.

Units of time are hours (hrs), minutes (min), or seconds(s)

How to Calculate Time when Speed and Distance are Given?

The boat travels at a speed of 40 kmph. How much time it will take to cover the distance of 120km?

Solution:

Let us write the given information.

Speed = 40kmph

Distance=120km

 So, the time is calculated as follows.

Thus, the time taken by the boat is 3 min.

Types of Speed

Uniform Speed

When an object travels the same distance in the same interval of time, then the speed of the object is called Uniform speed.

If a car is travelling at the rate of 50km/hr, it means that the car covers 50 kilometers every hour.

Non-Uniform Speed

When the speed of the body changes with respect to time then it is called

Non-uniform speed.

Running around the ground, initially one can run very fast. But later, when the energy level drops, and one cannot run as fast as compared to the previous one.

The speed in which the sea waves rise varies from time to time.

Average Speed

Average speed is the ratio of total distance travelled by the body to total time taken. 

Here, x and y are speeds, and the formula is applicable only when the body travels an equal distance each time.

How to Calculate the Average Speed?

A boat travels from one point to another point with a speed of 60km/hr and returns with a speed of 40km/hr. What is the average speed of the boat?

Solution:

Let us write the given information.

$\begin{array}{c}\text{Average speed=}\frac{2xy}{x+y}\\ =\frac{2\cdot 60\cdot 40}{60+40}\\ =48km/hr\end{array}$

The average speed is 48km/hr.

Distance - Time Graph

The graph of distance travelled versus the time taken is called the distance-time graph.

The graph is a straight line if the body is at a uniform speed. The graph is parallel to the time axis if the body is stationary. The graph is curve-shaped if the body is at non-uniform speed.

Some Examples on Speed, Distance, and Time

• Meena goes to college at a speed of 4km/hr and returns home at 3km/hr. It takes 4 hours to cover the total distance. What is the distance between college and home?

Solution:

Let x be the distance

So, time taken to travel from home to college =$\frac{x}{4}hr$.

Time taken to travel from college to home =$\frac{x}{3}hr$.

The total time taken by Meena is 4 hours.

Let us simplify the above equation to find the value of x.

The distance between home and college is 6.85km.

Formulas

$\text{Speed}=\frac{\text{Distance}}{\text{Time}}$

$\text{Distance}=\text{Speed}\times \text{Time}$

$\text{Time}=\frac{\text{Distance}}{\text{Speed}}$

Context and Applications:

This topic is significant in the professional exams for both undergraduate and graduate courses, especially for      

• Bachelor of Science in Mathematics
• Master of Science in Mathematics