What are Units and Measurements?
Measurements and comparisons are the foundation of science and engineering. We, therefore, need rules that tell us how things are measured and compared. For these measurements and comparisons, we perform certain experiments, and we will need the experiments to set up the devices.
A significant aspect of the scientific method is the results. The qualitative or quantitative methods of certain observations are the readings of experiments. Qualitative results are findings that do not have a related number. Numbers comprise a quantitative calculation dependent on observations. In their tests, scientists usually make quantitative measurements to take readings.
What are the Rules of Units and Measurements?
A quantity that can be directly or indirectly evaluated is called a physical quantity—for instance, length, area, volume, velocity, weight, etc. An accurate measurement is an essential part of an instrument that is associated with a collection of units for scientific observations. The outcome of a physical quantity calculation is represented entirely by a number or a numerical indicator following the measurement.
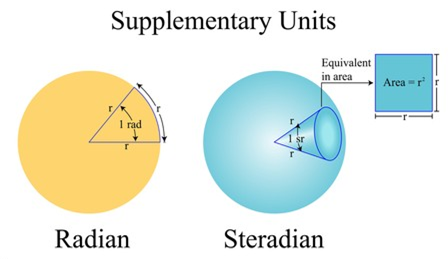
Supplementary Units
- Radian: The angle at the centre of a circle, measured in radians, is equal to the ratio of the length of the enclosed arc to the length of the circle's radius. Radian is the S.I. unit for measuring angles.
- Steradian: It is defined as the solid angle of a sphere subtended by a portion of the surface whose area is equal to the square of the sphere's radius.
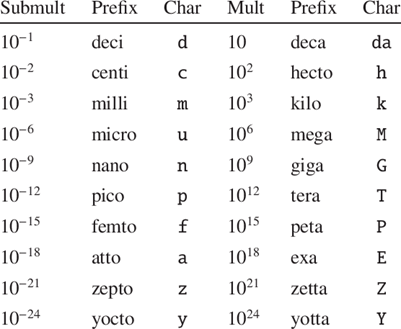
Common SI Prefixes and Symbols for Multiples and Submultiples
To express such large or small magnitudes, we use the following prefixes:
Now, suppose you use the measuring tape to calculate the length (physical quantity) of your dining table and express your answer as to say 2 meters. Your observation, then, 2 meters, implies a length that is twice the unit length of 1 meter. So here, 2 is the numerical value (n) of the quantity specified, and meter (u) is the unit of quantity.
Consider the length of the study table says it is 2 m, and it can also be represented as 200 cm. The unit used is cm, and the magnitude is 200 in this situation. Clearly, the smaller the unit size, the larger the numerical value associated with a given physical quantity calculation, which is the length.
We use various methods for calculating various length ranges. For example,
- A meter scale can measure the length between m to 1 m.
- Venire caliper can be used to measure smaller distances of the order of m.
- Screw gauge can measure lengths as small as m.
The length can be determined by these instruments in a restricted range. We do not employ these methods to measure very wide or very tiny magnitude distances.
To measure the distance between two planets, we use the special methods given below.
Measurement of Large Distances: Parallax Method
Parallax is characterized as the apparent change in a body's location with respect to a particular point in its history, with the sideways shift of the eye.
We observe it from two different locations (observatories) A and B on the Earth, separated by the parallax system, to calculate the distance D of planet S by the parallax method.
At the same time, as shown in the figure below, distance AB = b, We measure the angle between the two directions along which the planet is viewed at these two points. Therefore, θ is a very small angle. Then we approximately take A.B. as an arc of length b of a circle with Centre at P. The radius of the circle is D. Therefore, and the angle θ is given by:

Physics, focused on calculating physical quantities, is a quantitative science. As fundamental or base quantities, certain physical quantities have been selected. These are volume, mass, time, electric current, the temperature of thermodynamics, material quantity, and luminous strength.
- Each base quantity is specified in terms of a particular basic standard reference call.
- Other physical quantities derived from the base quantities will be expressed as a base unit mixture and are referred to as derived units. A complete set of units is called a system of units, both fundamental and derived.
- Centered on seven base units, the International System of Units (S.I.) is currently a globally agreed system and is commonly used.
- The SI units, for both the base quantities and the derived quantities obtained from them, are used in all physical measurements. Via SI units with special names, some derived units are expressed (such as joule, newton, watt, etc.).
- The SI units have well-defined and internationally accepted unit symbols (such as m for meter, kg for kilogram, s for second, A for ampere, N for newton, etc.). Direct and indirect methods are used for the measurement of physical quantities.
Thus, in expressing a physical quantity, we choose a unit and then find how many times that unit is contained in the given physical quantity:
Physical quantity (Q) = Magnitude × Unit =n × u
Where n represents the numerical value, and u represents the unit.
Therefore, physical quantity can also be described as
∴ n ∝1/u
Or n*u = constant
Types of Physical Quantities
Scalar Quantities
Scalar quantities are called quantities that only have magnitude. They don't have direction r. For example, scalar quantities are distance travelled, time interval, speed, energy, mass. Scalars are described by real numbers that are usually but not necessarily positive.
It is possible to add or subtract scalar quantities algebraically.
Vector Quantities
Other quantities, such as force and velocity, have both magnitude and direction and are called vectors. For example, vector quantities are displacement, velocity, acceleration. It is also specified by a number along with the direction and unit.
According to the vector addition rules, vector quantities may be added or subtracted. Such rules are distinct from algebraic addition laws.
Fundamental and Derived Quantities
The International System of Units is used by physicists around the world (also called the S.I.). S.I. is essentially a metric system, which is useful since powers of 10 are associated with units of different sizes. Like other physical quantities, the system has physical norms for length, mass, and time. These are called basic units since they are recognized globally accepted.
There are many physical quantities, but not all are separate. Physical quantities are divided into two categories: basic quantities and derived quantities.
Fundamental or Essential Quantities
There are only a few independent quantities out of a vast number of physical quantities that occur in nature and do not need the assistance of any other physical quantity for their description. These are also called essential or fundamental quantities as all other quantities are centered on and can be articulated in terms of these quantities.
| Fundamental Quantity | S. I Unit | ||
| Name | Symbol | Name | Symbol |
| Mass | m | Kilogram | kg |
| Length | l | Meter | m |
| Time | t | Second | s |
| Current | I | Ampere | A |
| Temperature | T | Kelvin | K |
| Amount of Substance | n | Mole | mol |
| Luminous Intensity | Iv | Candela | cd |
Quantities Derived
All other physical quantities are a mixture of fundamental quantities. Therefore, these are called quantities derived.
Example: Speed is the length to time ratio. So, quantity is derived. It is defined in terms of the length and time of the base quantities and their base standards.
| Derived Quantity | S. I. Unit | ||
| Name | Symbol | Name | Symbol |
| Displacement | d | Meter | m |
| Area | A | meter squared | m2 |
| Volume | V | meter cubed | m3 |
| Speed | s | meter/second | m/s |
| Velocity | v | meter/second | m/s |
| Acceleration | a | meter/second2 | m/s2 |
| Force | F | Newton | N=kg m/s2 |
| Energy | E | Joule | J = Nm |
| Density | ρ | kilogram / meter cubed | kg/m3 |
| Moment | T | newton meter | N m |
| Power | P | Watt | W = N m/s |
| Work | W | Joule | J = Nm |
| Momentum | ρ | kilogram meter /second | kg m/s = Ns |
| Pressure | P | Pascal | Pa = N/m2 |
System of Units
S.I. is the abbreviation for the International System of Units. In this system, there are seven fundamental quantities and two supplementary units.
Common Mistakes
- Before you make a set of measurements, you need to know what the measurements are for and hence understand the uncertainty of the measurement you are looking for.
- You must understand how many times should the calculation be repeated, along with the acceptance criteria (for example, tolerance) for the outcome.
- You will have to be certain that you're going to make the right measurements.
- Use proper tools.
Context and Applications
This topic is significant in the professional exams for both undergraduate and graduate courses, especially for
- 10th,11th,12th Standard.
- Engineering Students
- Medical Students
Units and measurements play an important role in the everyday life of every individual.
Related Concepts
- Accuracy
- Error
- Precision
- Dimensions
Want more help with your algebra homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Units and Measurements Homework Questions from Fellow Students
Browse our recently answered Units and Measurements homework questions.