40 14 Mo Β 3 C L. L/2
Automotive Technology: A Systems Approach (MindTap Course List)
6th Edition
ISBN:9781133612315
Author:Jack Erjavec, Rob Thompson
Publisher:Jack Erjavec, Rob Thompson
Chapter23: Electrical Accessories
Section: Chapter Questions
Problem 6RQ: Name the two most common problems that occur with power seats.
Related questions
Question
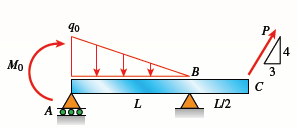
Find support reactions at A and B and then
calculate the axial force N, shear force V, and bending
moment M at mid-span of AB. Let L = 4 m,
q0 = 160 N/m, P = 200 N, and M0 = 380 N . m.
Transcribed Image Text:40
14
Mo
Β
3
C
L.
L/2
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 1 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Recommended textbooks for you

Automotive Technology: A Systems Approach (MindTa…
Mechanical Engineering
ISBN:
9781133612315
Author:
Jack Erjavec, Rob Thompson
Publisher:
Cengage Learning

Automotive Technology
Mechanical Engineering
ISBN:
9781337794213
Author:
ERJAVEC, Jack.
Publisher:
Cengage,

Automotive Technology: A Systems Approach (MindTa…
Mechanical Engineering
ISBN:
9781133612315
Author:
Jack Erjavec, Rob Thompson
Publisher:
Cengage Learning

Automotive Technology
Mechanical Engineering
ISBN:
9781337794213
Author:
ERJAVEC, Jack.
Publisher:
Cengage,