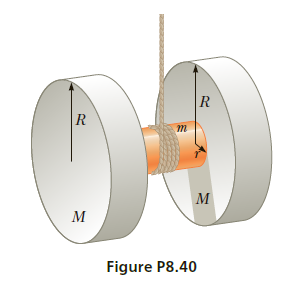
An oversized yo-yo is made from two identical solid disks
each of mass M= 2.00 kg and radius R = 10.0 cm. The two
disks are joined by a solid cylinder of radius r = 4.00 cm and
mass m = 1.00 kg as in Figure P8.40. Take the center of the
cylinder as the axis of the system, with positive torques directed
to the left along this axis. All torques and angular variables
are to be calculated around this axis. Light string is wrapped
around the cylinder, and the system is then allowed to drop
from rest. (a) What is the moment of inertia of the system?
Give a symbolic answer. (b) What torque does gravity exert on
the system with respect to the given axis? (c) Take downward as
the negative coordinate direction. As depicted in Figure P8.40,
is the torque exerted by the tension positive or negative? Is
the
translational acceleration? (d) Write an equation for the angular
acceleration ∝ in terms of the translational acceleration ∝ in terms of the translational acceleration a and radius r. (Watch the sign!) (e) Write Newton’s second lawfor the system in terms of m, M, a, T, and g. (f) Write Newton’s second law for rotation in terms of I, ∝, T, and r. (g) Eliminate
∝ from the rotational second law with the expression found in
part (d) and find a symbolic expression for the acceleration a
in terms of m, M, g, r, and R. (h) What is the numeric value for
the system’s acceleration? (i) What is the tension in the string?
( j) How long does it take the system to drop 1.00 m from rest?
Trending now
This is a popular solution!
Step by step
Solved in 4 steps with 2 images









