What is Torque?
Torque is the rotational equivalent of linear force in physics and mechanics. Based on the course of study, it is also known as the moment of force, rotational force, or turning effect.
Torque is a vector quantity that is used to calculate a force's tendency to produce a rotational effect in an object about some axis. The point where the object rotates is called the axis of rotation. The direction of the torque vector is determined by the direction of the force on the axis.
Moment Arm Formula
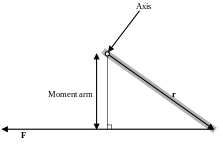
The "moment arm" is demonstrated in the figure to the right, along with the vectors r and F mentioned earlier. The issue with this definition is that it does not provide the direction of the torque but only the magnitude, making it difficult to apply in three-dimensional cases. The moment arm equals the distance to the center when the force is perpendicular to the displacement vector r, and the torque is maximum for the given force. The formula for calculating the magnitude of a torque caused by a perpendicular force:
τ=(moment arm)(force)
The magnitude of the torque can be calculated by first determining the lever arm and then multiplying it by the applied force. The perpendicular distance between the axis of rotation and the force's line of action is defined as the lever arm.
To calculate the magnitude of the torque, first, compute the lever arm and then multiply it by the applied force. Based on the foregoing, we can conclude that torque generated is proportional to the magnitude of the force and the perpendicular distance between the point about which torque is calculated and the point at which force is applied. The direction of the torque may be clockwise or anticlockwise depending on the direction of applied force. Positive torque causes an object to rotate counter clockwise. A negative torque rotates an object clockwise.
As a result, torque is mathematically represented as:
τ = F.r. sinθ

Where r denotes the moment arm's length and θ denotes the angle formed by the force vector and the moment arm.
The SI unit for torque is the Newton-meter. Using the right-hand rule, we can determine the direction of the torque vector. Our thumb will point in the direction of the torque vector if we point our fingers in the direction of r and curl them in the direction of F.
In imperial units, the Foot-pound is often used. Pound-force is the amount of force exerted by earth gravity on a one-pound object. The magnitude of these units is frequently similar as
1 Nm≃1.74 ft⋅lbs
Balanced Torques
When the torques on either side of a fulcrum are equal, the torques are said to be balanced. A common example of balanced torques is two children on a see-saw. If the see-saw's fulcrum is in the centre, the two children must have an equal mass for the see-saw to be balanced. If the fulcrum is not located in the centre, their masses must differ to produce equal torques.
Types of Torques
Torque can be both static and dynamic. Static torque is defined as torque that does not produce angular acceleration. Here are some examples of static torque:
- When a person pushes a closed door, he or she is using the door is static that does not rotate despite the force applied. Because there is no acceleration, pedaling a bicycle at a constant speed is another example of static torque.
- The drive shaft in a racing car accelerating from the start line generates dynamic torque because it must generate angular acceleration of the wheels due to the car's acceleration along the track.
Torque in Rotational Kinematics
For a rotational system, Newton's first law is equivalent to the concept of rotational equilibrium. Unless acted on by an external torque, an object that is not rotating remains so. Similarly, an object rotating at constant angular velocity continues to rotate unless acted on by an external torque.
However, if the rotational speed is known, power can be calculated from torque. In fact, an engine's horsepower is calculated using measured torque and rotational speed. Horsepower measures the overall efficiency of an engine. Torque is a simple measurement of the maximum twisting force that an engine can produce when it is worked hard.
Angular Momentum
Torque and angular momentum are closely linked. Angular momentum, denoted by the letter ‘L,' is the rotational analogue of linear momentum ‘p.' It's a vector. The particle's angular momentum is
L = r × p L = r p sinθ
where, θ is the angle between r and p.
Relation between Angular Momentum & Torque
Now let’s find the formula or expression.
Rate of change of Angular Momentum with time = ΔL/ΔT
Now,
ΔL/ΔT = Δ(I ω)/ΔT = I. Δω/ΔT ……. (1)
Here I will be a constant for a particular object.
Now Δω/ΔT ( angular velocity by time) is angular acceleration (α).
So from equation 1, we can write, ΔL/ΔT = I α…………………(2)
I (moment of inertia) is the rotational counterpart of mass (inertia). Torque (τ) refers to the moment of force. τ = r x F = r F sinθ……………. (3)
F is the force vector and r refers to the position vector
θ happens to be the angle between the force vector and the lever arm vector. ‘x’ certainly denotes the cross product.
τ = r F sin θ = r ma sinθ = r m αr sinθ = mr2. αsinθ = I αsinθ = I x α ……………………… (4)
[α is angular acceleration, I stands for the moment of inertia, and x stands for cross product.]
τ= I α(from equation 4)
This means that torque produced depends on the moment of inertia and angular acceleration
So from equation 2 one can get, ΔL/ΔT = τ……………………. (5)
Torque is, without a doubt, the rate of change of angular momentum with time.
Also, τ= I α
or, τ= I (ω2-ω1)/t [here α = angular acceleration = time rate of change of the important angular velocity = (ω2 – ω1)/t where ω2 and ω1 happen to be the final and initial angular velocities and t is the time gap]
or, τ t = I (ω2-ω1) ……………………(6)
when, τ= 0 (i.e., net torque is zero),
I (ω2-ω1) = 0
i.e., I ω2=I ω1 ………….. (7)
Common Mistakes
- ·People frequently overlook the fact that angular acceleration can be zero. When an object's torques cancel out, the net torque and angular acceleration are both zero.
- Another common misunderstanding is that the torques only add up to zero around the fulcrum.
Context & Applications
This topic is significant in the professional exams for both undergraduate and graduate courses, especially for
- 10th,11th,12th Standard.
- Engineering Students
- Torque is a factor in several complicated machines, including the electric motor that powers most household appliances. It is particularly essential to the operation of automobiles, where it plays a key role in the engine and transmission.
Related Concepts
- Friction Torque
- Static equilibrium
- Pseudovector
- Translational Equilibrium
Want more help with your physics homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Torque Homework Questions from Fellow Students
Browse our recently answered Torque homework questions.