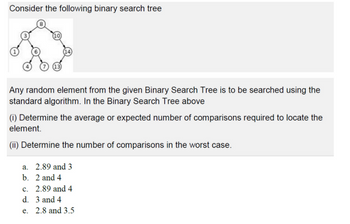
Consider the following binary search tree Any random element from the given Binary Search Tree is to be searched using the standard algorithm. In the Binary Search Tree above (i) Determine the average or expected number of comparisons required to locate the element. (ii) Determine the number of comparisons in the worst case.

Generate the decision tree for sorting the following sequence 50, 100, 150 with all its possible permutations

In the worst-case scenario, binary tree sort employing a self-balancing binary search tree requires O(n log n) time.

Let T be a binary search tree with n nodes, in which n > 0. When T is linear, the search algorithm makes key comparisons, in the unsuccassful case.

Kruskal's Algorithm: Kruskal's algorithm is a minimum-spanning-tree algorithm which finds an edge of the least possible weight that connects any two trees in the forest. This algorithm is a Greedy Algorithm. The steps to find a MST using this algorithm are as follows: Sort all the edges in non-decreasing order of their weight. Pick the smallest edge. Check if it forms a cycle with the spanning tree formed so far. If cycle is not formed, include this edge. Else, discard it. Repeat step2 until there are (V-1) edges in the spanning tree. Example with 10 vertices and 20 weighted edges:

Using a self-balancing binary search tree, binary tree sort is nevertheless slower than merge sort, taking O(n log n) time in the worst case.

In a binary search tree, to remove a node N that has parent P and one child C, we do the following:   Group of answer choices If C is the right child of N, we make C the right child of P, and if C is the left child of N, we make C the left child of P   If C is the right child of N, we make C the left child of P, and if C is the left child of N, we make C the right child of P   If N is the left child of P, we make C the left child of P and if N is the right child of P, we make C the right child of P   If N is the left child of P, we make C the right child of P and if N is the right child of P, we make C the left child of P   none of the above

In the worst-case scenario, binary tree sort employing a self-balancing binary search tree requires O(n log n) time, which is slower than merge sort.

Binary tree sort employing a self-balancing binary search tree takes O(n log n) time in the worst scenario, slower than merge sort.

In the worst-case situation, binary tree sort using a self-balancing binary search tree requires O(n log n) time, which is slower than merge sort.