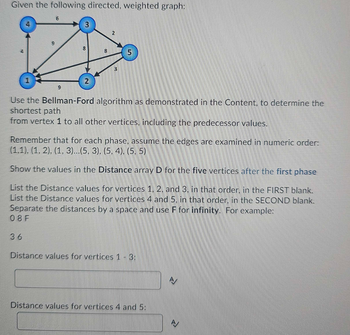
Given the following directed, weighted graph: 9 6 36 9 3 2 8 3 5 Use the Bellman-Ford algorithm as demonstrated in the Content, to determine the shortest path from vertex 1 to all other vertices, including the predecessor values. Remember that for each phase, assume the edges are examined in numeric order: (1,1), (1, 2), (1, 3)...(5, 3), (5, 4), (5, 5) Show the values in the Distance array D for the five vertices after the first phase List the Distance values for vertices 1, 2, and 3, in that order, in the FIRST blank. List the Distance values for vertices 4 and 5. in that order, in the SECOND blank. Separate the distances by a space and use F for infinity. For example: 08 F Distance values for vertices 1 - 3: Distance values for vertices 4 and 5: >

1. Consider the weighted, directed graph containing the following vertices and edges.(Weights are in the parentheses.)Vertices: {A, B, C, D} Edges: {AB(5), BC(3), CA(4), AD(2), DA(4), CB(3)}a. Starting at vertex C, determine the shortest path tree using Dijkstrab. If you were to apply Floyd-Warshall’s algorithm to this tree, would it include the shortest path tree you found using Dijkstra? Why or why not?c. Starting at vertex C, determine the minimum spanning tree using Prim.d. Would Kruskal’s algorithm always result in the same MST as Prim’s? Why or why not?   Please provide graphs if possible.

Please explain what it means to: Model relationships using graphs Use Fleury's Algorithm to find possible Euler paths   Use Fleury's Algorithm to find possible Euler circuit Please provide examples of your answers.

Determine whether a graph with the given adjacency matrix is bipartite.