
Database System Concepts
7th Edition
ISBN: 9780078022159
Author: Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan
Publisher: McGraw-Hill Education
expand_more
expand_more
format_list_bulleted
Concept explainers
Question
If A is NP-complete, and A has a polynomial time
For example, the four vertices u2, u3,u5, and u6 form the largest clique in the graph below.
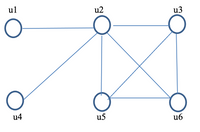
Transcribed Image Text:ul
u2
u3
u4
u5
u6
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 1 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, computer-science and related others by exploring similar questions and additional content below.Similar questions
- Recall the Floyd-Warshall algorithm. For this problem, we are interested in the number of paths between each pair of vertices i and j in a directed acyclic graph. Suppose we know the number of paths between each pair of vertices where we restrict the intermediate vertices to be chosen from 1, 2, . . . , k − 1, show how we can extend the result to allow vertex k as an intermediate vertex as well. To conclude what would its complexity be?arrow_forwardLet G be a undirected connected graph where the cost/length of every edge is 1 unit. Let s, tı, t2 be three distinct nodes. Describe shortly and in natural language (English) an O(m) algorithm that finds a node u such that the distance of u from s is as large as possible, but the length of any path from s to tį and from s to t2 that contains u is no greater from the respective distances of s from t1 and t2 (m is the number of edges; also let n be the number of nodes). Problem 1 Hint: Run three BFS searches.arrow_forwardSuppose you are given a directed graph G on n vertices, each of which is assigned a colour. (In this problem, both endpoints of an edge can have the same colour.) Give an efficient algorithm to find the length of the longest monochromatic directed walk in G. (In a walk we can revisit vertices and recross edges, whereas in a path we cannot.) Your algorithm should return "undefined" if there is a directed cycle whose vertices are all the same colour.arrow_forward
- Let G be a graph, where each edge has a weight. A spanning tree is a set of edges that connects all the vertices together, so that there exists a path between any pair of vertices in the graph. A minimum-weight spanning tree is a spanning tree whose sum of edge weights is as small as possible. Last week we saw how Kruskal's Algorithm can be applied to any graph to generate a minimum-weight spanning tree. In this question, you will apply Prim's Algorithm on the graph below. You must start with vertex A. H 4 4 1 3 J 2 C 10 4 8 B 9 F 18 8 There are nine edges in the spanning tree produced by Prim's Algorithm, including AB, BC, and IJ. Determine the exact order in which these nine edges are added to form the minimum-weight spanning tree. 3.arrow_forwardMost graph algorithms that take an n×n adjacency-matrix representation as input require at least time O(n^2), but there are some exceptions. Show how to determine whether a simple directed graph G contains a universal sink, that is, a vertex with in degree n − 1 and out-degree 0, in time O(n) given an n × n adjacency matrix for G. (A vertex v has indegree k if there are precisely k edges of the form (u, v), and has outdegree k if there are precisely k edges of the form (v, u).)arrow_forwardGiven a digraph, find a bitonic shortest path from s to every other vertex (if one exists). A path is bitonic if there is an intermediate vertex v suchthat the edges on the path from s to v are strictly increasing and the edges on the pathfrom v to t are strictly decreasing. The path should be simple (no repeated vertices).arrow_forward
- Shortest paths. Let G = (V,E) be an acyclic weighted directed graph and let s ∈ V be an arbitrary vertex. Describe an algorithm which in time O(|V | + |E|) finds shortest paths from s to all (reachable from s) vertices in the graph G, represented by an adjacency list.arrow_forwardDiscrete mathematics. Let G = (V, E) be a simple graph4 with n = |V| vertices, and let A be its adjacency matrix of dimension n × n. We want to count the L-cycles : such a cycle, denoted by C = u0u1 · · · uL with uL = u0 contains L distinct vertices u0, . . . , uL-1 et L edges E(C) = {uiui+1 | 0 ≤ i ≤ L − 1} ⊆ E. Two cycles are distinct if the edge sets are different : C = C' if and only if E(C) = E(C'). We define the matrices D, T, Q, the powers of A by matrix multiplication : D = A · A = A2, T = A · D = A3, Q = A · T = A4. Consider the values on the diagonals. Prove that the number of 3-cycles N3 in the whole graph is N3 = 1/6 ∑ u∈V Tu,uarrow_forwardLet G be a graph with V vertices and E edges. One can implement Kruskal's Algorithm to run in O(E log V) time, and Prim's Algorithm to run in O(E + V log V) time. If G is a dense graph with an extremely large number of vertices, determine which algorithm would output the minimum-weight spanning tree more quickly. Clearly justify your answer.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Database System ConceptsComputer ScienceISBN:9780078022159Author:Abraham Silberschatz Professor, Henry F. Korth, S. SudarshanPublisher:McGraw-Hill Education
Database System ConceptsComputer ScienceISBN:9780078022159Author:Abraham Silberschatz Professor, Henry F. Korth, S. SudarshanPublisher:McGraw-Hill Education Starting Out with Python (4th Edition)Computer ScienceISBN:9780134444321Author:Tony GaddisPublisher:PEARSON
Starting Out with Python (4th Edition)Computer ScienceISBN:9780134444321Author:Tony GaddisPublisher:PEARSON Digital Fundamentals (11th Edition)Computer ScienceISBN:9780132737968Author:Thomas L. FloydPublisher:PEARSON
Digital Fundamentals (11th Edition)Computer ScienceISBN:9780132737968Author:Thomas L. FloydPublisher:PEARSON C How to Program (8th Edition)Computer ScienceISBN:9780133976892Author:Paul J. Deitel, Harvey DeitelPublisher:PEARSON
C How to Program (8th Edition)Computer ScienceISBN:9780133976892Author:Paul J. Deitel, Harvey DeitelPublisher:PEARSON Database Systems: Design, Implementation, & Manag...Computer ScienceISBN:9781337627900Author:Carlos Coronel, Steven MorrisPublisher:Cengage Learning
Database Systems: Design, Implementation, & Manag...Computer ScienceISBN:9781337627900Author:Carlos Coronel, Steven MorrisPublisher:Cengage Learning Programmable Logic ControllersComputer ScienceISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Programmable Logic ControllersComputer ScienceISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education

Database System Concepts
Computer Science
ISBN:9780078022159
Author:Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan
Publisher:McGraw-Hill Education

Starting Out with Python (4th Edition)
Computer Science
ISBN:9780134444321
Author:Tony Gaddis
Publisher:PEARSON

Digital Fundamentals (11th Edition)
Computer Science
ISBN:9780132737968
Author:Thomas L. Floyd
Publisher:PEARSON

C How to Program (8th Edition)
Computer Science
ISBN:9780133976892
Author:Paul J. Deitel, Harvey Deitel
Publisher:PEARSON

Database Systems: Design, Implementation, & Manag...
Computer Science
ISBN:9781337627900
Author:Carlos Coronel, Steven Morris
Publisher:Cengage Learning

Programmable Logic Controllers
Computer Science
ISBN:9780073373843
Author:Frank D. Petruzella
Publisher:McGraw-Hill Education