Database System Concepts
7th Edition
ISBN: 9780078022159
Author: Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan
Publisher: McGraw-Hill Education
expand_more
expand_more
format_list_bulleted
Related questions
Concept explainers
Question
Transcribed Image Text:1) Build Heap - Diagramming
grisenT-9917 ro1692 vienis (S
Perform the Build Heap algorithm on the following array to output a Min heap. Draw the array
following each downheap at the given index in the algorithm. Write your final answer in the Output
row of the table.
index 4
index 3
index 2
index 1
Output:
0
null
1
70
2
20
3
10
4
45
(37
(da
5
30
6
15
Do not write below this line. It may not be scanned, therefore it will not be graded.
7
5
8
25
3A
Expert Solution
arrow_forward
Step 1
Solution-
A binary tree that meets the heap property is referred to as a heap. There are two types of heaps:
The element at each node is greater than or equal to the element at its parent, according to the minimum heap. At the root is the element with the lowest value.
Max heap: Each node's element is smaller than the element at its parent. The root/parent element has the greatest value.
The term "heap" will always refer to min-heap via this image.
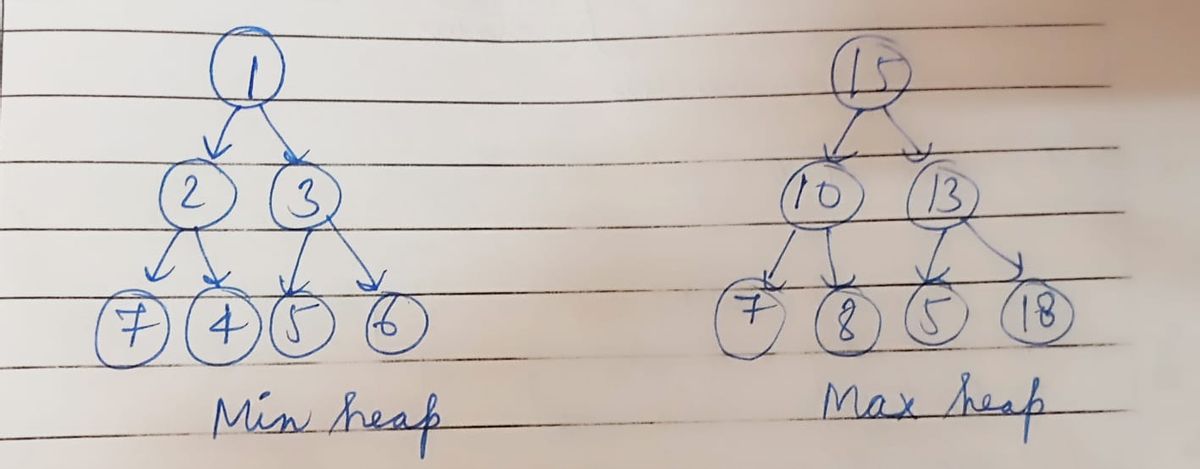
The lowest (or highest) priority element is always stored at the root of a heap, hence the name. Although it can be considered partially ordered, a heap is not a sorted structure. The aforementioned photos demonstrate that there is no clear hierarchy among the nodes at any level.
When you need to get rid of something of the lowest (or highest) priority, a heap comes in handy. Implementing a priority queue is one frequent usage of a heap.
Step by stepSolved in 4 steps with 6 images
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, computer-science and related others by exploring similar questions and additional content below.Similar questions
- If the last digit of your Kean ID is odd, implement a program that randomly generates 100,000 integers and sorts them using Heap sort. Implement, calculate, and provide its execution timearrow_forwardPlease justify your answer: Some sorting algorithms require extra space, apart from the space needed for the original array that needs to be sorted. Which one of the following statements on the space usage of sorting algorithms is correct? a.) A Heapsort for sorting an array of size N requires an amount of extra space proportional to N. b.) Insertion Sort for sorting an array of size N requires an amount of extra space proportional to N. c.) Merge sort for sorting an array of size N requires an amount of extra space proportional to N. d.) Quicksort for sorting an array of size N requires an amount of extra space proportional to N. e.) None of the abovearrow_forwardALGORITHM Quicksort(A[l..r])//Sorts a subarray by quicksort//Input: Subarray of array A[0..n − 1], defined by its left and right// indices l and r//Output: Subarray A[l..r] sorted in nondecreasing order if l < r s = Partition(A[l..r]) //s is a split position Quicksort(A[l..s − 1]) Quicksort(A[s + 1..r]) The above code is the quicksort algorithm.Perform a time complexity analysis for quicksort. You need to explain 1) what makes a worst case, what makes a best case, 2) the time complexity for both the worst case and the best case, 3) how to avoid the worst case in practice.arrow_forward
- USING C LANGUAGE IN NETBEANS : Write a program menu that creates and manages Fibonacci heaps. The program must implement the following operations: creation, insertion, find min, extract min, decrease key, and deletion. **NOTE: The program should present a menu where user may choose from implemented options.arrow_forwardWe push all the elements of an array A in order (starting from index 0 of the array A) into a stack. We then pop all the elements from the stack and store them in order (starting from index 0) in A. Which of the following is true after all pop operations complete? O The elements of A are reversed Each element of A is in its original location O The elements of A are in random new locations The array A is empty O None of the abovearrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
- Database System ConceptsComputer ScienceISBN:9780078022159Author:Abraham Silberschatz Professor, Henry F. Korth, S. SudarshanPublisher:McGraw-Hill Education
Starting Out with Python (4th Edition)Computer ScienceISBN:9780134444321Author:Tony GaddisPublisher:PEARSON
Digital Fundamentals (11th Edition)Computer ScienceISBN:9780132737968Author:Thomas L. FloydPublisher:PEARSON 
C How to Program (8th Edition)Computer ScienceISBN:9780133976892Author:Paul J. Deitel, Harvey DeitelPublisher:PEARSON
Database Systems: Design, Implementation, & Manag...Computer ScienceISBN:9781337627900Author:Carlos Coronel, Steven MorrisPublisher:Cengage Learning
Programmable Logic ControllersComputer ScienceISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Database System Concepts
Computer Science
ISBN:9780078022159
Author:Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan
Publisher:McGraw-Hill Education
Starting Out with Python (4th Edition)
Computer Science
ISBN:9780134444321
Author:Tony Gaddis
Publisher:PEARSON
Digital Fundamentals (11th Edition)
Computer Science
ISBN:9780132737968
Author:Thomas L. Floyd
Publisher:PEARSON
C How to Program (8th Edition)
Computer Science
ISBN:9780133976892
Author:Paul J. Deitel, Harvey Deitel
Publisher:PEARSON
Database Systems: Design, Implementation, & Manag...
Computer Science
ISBN:9781337627900
Author:Carlos Coronel, Steven Morris
Publisher:Cengage Learning
Programmable Logic Controllers
Computer Science
ISBN:9780073373843
Author:Frank D. Petruzella
Publisher:McGraw-Hill Education