
Computer Networking: A Top-Down Approach (7th Edition)
7th Edition
ISBN: 9780133594140
Author: James Kurose, Keith Ross
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Question
in C++

Transcribed Image Text:Question: In Calculus you will learn an algorithm called Newton's Method for finding the roots of a
equation f(x) = 0. The technique starts from an initial guess x1 and computes a next estimate x2 by:
f (x1)
f'(x1)
X2 = x1
We then apply the procedure again starting from x2 (in place of x1 in the right-hand-side) and we
keep repeating this until successive estimates differ by less than some preset tolerance. Note that each
repetition is called an iteration.
Write a program called root.c which finds a root of the function f(x) = sin x
of the user provided starting guess x1.
Your program must consist of a main program, which opens the output file rootout.txt for ap-
pending (mode = "a"), reads the initial guess (x1) and desired error tolerance (tol) from the user,
calls the function newton (), described below, and writes the estimated root (root) and number of
iterations(iter) required to the output file. Aside from the main, your program must consist of the
following three functions;
- 2e-* in the vicinity
• f() which takes an argument x and returns f(x) = sin(x) – 2e¬ª,
• df () which takes an argument x and returns f'(x) = cos(x) + 2e-ª
• newton () which takes the initial guess x1 and the desired tolerance tol as arguments and
calculates and sets (in main) both the estimated root (root) and the number of iterations
(iter) required to find this root within the desired tolerance. Assume that the tolerance in this
case refers to an absolute tolerance, i.e. quit when x2 – x1| < tol.
- r.
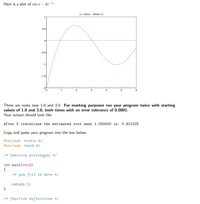
Transcribed Image Text:Here is a plot of sin x – 2e-*:
y = sin(x) – 2exp(-x)
0.5
-0.5
-1
-1.5
3
4
There are roots near 1.0 and 3.0. For marking purposes run your program twice with starting
values of 1.0 and 3.0, both times with an error tolerance of 0.0001.
Your output should look like:
After 3 iterations the estimated root near 1.000000 is: 0.921025
Copy and paste your program into the box below.
#include <stdio.h>
#include <math.h>
/* function prototypes */
int main(void)
/* you fill in here */
return 0;
}
/* function definitions */
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps

Knowledge Booster
Similar questions
Recommended textbooks for you
 Computer Networking: A Top-Down Approach (7th Edi...Computer EngineeringISBN:9780133594140Author:James Kurose, Keith RossPublisher:PEARSON
Computer Networking: A Top-Down Approach (7th Edi...Computer EngineeringISBN:9780133594140Author:James Kurose, Keith RossPublisher:PEARSON Computer Organization and Design MIPS Edition, Fi...Computer EngineeringISBN:9780124077263Author:David A. Patterson, John L. HennessyPublisher:Elsevier Science
Computer Organization and Design MIPS Edition, Fi...Computer EngineeringISBN:9780124077263Author:David A. Patterson, John L. HennessyPublisher:Elsevier Science Network+ Guide to Networks (MindTap Course List)Computer EngineeringISBN:9781337569330Author:Jill West, Tamara Dean, Jean AndrewsPublisher:Cengage Learning
Network+ Guide to Networks (MindTap Course List)Computer EngineeringISBN:9781337569330Author:Jill West, Tamara Dean, Jean AndrewsPublisher:Cengage Learning Concepts of Database ManagementComputer EngineeringISBN:9781337093422Author:Joy L. Starks, Philip J. Pratt, Mary Z. LastPublisher:Cengage Learning
Concepts of Database ManagementComputer EngineeringISBN:9781337093422Author:Joy L. Starks, Philip J. Pratt, Mary Z. LastPublisher:Cengage Learning Prelude to ProgrammingComputer EngineeringISBN:9780133750423Author:VENIT, StewartPublisher:Pearson Education
Prelude to ProgrammingComputer EngineeringISBN:9780133750423Author:VENIT, StewartPublisher:Pearson Education Sc Business Data Communications and Networking, T...Computer EngineeringISBN:9781119368830Author:FITZGERALDPublisher:WILEY
Sc Business Data Communications and Networking, T...Computer EngineeringISBN:9781119368830Author:FITZGERALDPublisher:WILEY

Computer Networking: A Top-Down Approach (7th Edi...
Computer Engineering
ISBN:9780133594140
Author:James Kurose, Keith Ross
Publisher:PEARSON

Computer Organization and Design MIPS Edition, Fi...
Computer Engineering
ISBN:9780124077263
Author:David A. Patterson, John L. Hennessy
Publisher:Elsevier Science

Network+ Guide to Networks (MindTap Course List)
Computer Engineering
ISBN:9781337569330
Author:Jill West, Tamara Dean, Jean Andrews
Publisher:Cengage Learning

Concepts of Database Management
Computer Engineering
ISBN:9781337093422
Author:Joy L. Starks, Philip J. Pratt, Mary Z. Last
Publisher:Cengage Learning

Prelude to Programming
Computer Engineering
ISBN:9780133750423
Author:VENIT, Stewart
Publisher:Pearson Education

Sc Business Data Communications and Networking, T...
Computer Engineering
ISBN:9781119368830
Author:FITZGERALD
Publisher:WILEY