
Database System Concepts
7th Edition
ISBN: 9780078022159
Author: Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan
Publisher: McGraw-Hill Education
expand_more
expand_more
format_list_bulleted
Question
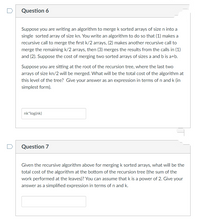
Transcribed Image Text:Question 6
Suppose you are writing an algorithm to merge k sorted arrays of size n into a
single sorted array of size kn. You write an algorithm to do so that (1) makes a
recursive call to merge the first k/2 arrays, (2) makes another recursive call to
merge the remaining k/2 arrays, then (3) merges the results from the calls in (1)
and (2). Suppose the cost of merging two sorted arrays of sizes a and b is a+b.
Suppose you are sitting at the root of the recursion tree, where the last two
arrays of size kn/2 will be merged. What will be the total cost of the algorithm at
this level of the tree? Give your answer as an expression in terms of n and k (in
simplest form).
nk*log(nk)
Question 7
Given the recursive algorithm above for merging k sorted arrays, what will be the
total cost of the algorithm at the bottom of the recursion tree (the sum of the
work performed at the leaves)? You can assume that k is a power of 2. Give your
answer as a simplified expression in terms of n and k.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 1 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, computer-science and related others by exploring similar questions and additional content below.Similar questions
- Consider a scenario in which you are presented with a data set of length K. Write a simple recursive algorithm to choose all possible pairs of elements in the set. Assess the computational complexity and explain your calculations.arrow_forwardMerge sort is an efficient sorting algorithm with a time complexity of O(n log n). This means that as the number of elements (chocolates or students) increases significantly, the efficiency of merge sort remains relatively stable compared to other sorting algorithms. Merge sort achieves this efficiency by recursively dividing the input array into smaller sub-arrays, sorting them individually, and then merging them back together. The efficiency of merge sort is primarily determined by its time complexity, which is , where n is the number of elements in the array. This time complexity indicates that the time taken by merge sort grows logarithmically with the size of the input array. Therefore, even as the number of chocolates or students increases significantly, merge sort maintains its relatively efficient performance. Regarding the distribution of a given set of x to y using iterative and recursive functions, the complexity analysis depends on the specific implementation of each…arrow_forwardQuestion Which of the following statements about mergesort are true? Unless otherwise specified, assume that mergesort refers to the pure recursive (top-down) version of mergesort (with no optimizations), using the merging subroutine described in lecture. Answer Mark all that apply. OThe number of compares to bottom-up mergesort an array depends only on the length of the array n (and not on the keys or order of the keys in the array). O Mergesort is a stable sorting algorithm. Suppose that n is a power of 2. For any array of n distinct keys, top-down mergesort and bottom-up mergesort compare exactly the same pairs of keys (but possibly in a different order). OMergesort uses only a logarithmic amount of space (other than the input array). OIt is possible to design a compare-based algorithm to merge any two sorted arrays, each of length n, with no more than 3/2 n compares.arrow_forward
- Java: Consider the following algorithm for searching in an unsorted array. If the size of the array is 1, then check if it contains the element to be searched. Otherwise, divide the array into two halves, and recursively search both halves. Which of (a)–(c) is false? The running time of this algorithm is O(N) The actual running time of this algorithm is likely to be better than sequential search. This is an example of a divide‐and‐conquer algorithm all of the above are true none of the above is truearrow_forwardUse Binary Search, Recursive (Algorithm 2.1) to search for the integer 120 in the following list (array) of integers. Show the actions (execution) step by step. No code needed. Solution: 12 34 37 45 57 82 99 120 134 1. Compute the middle index from initial low (1) and high (9) indices: mid = Continue... Aarrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Database System ConceptsComputer ScienceISBN:9780078022159Author:Abraham Silberschatz Professor, Henry F. Korth, S. SudarshanPublisher:McGraw-Hill Education
Database System ConceptsComputer ScienceISBN:9780078022159Author:Abraham Silberschatz Professor, Henry F. Korth, S. SudarshanPublisher:McGraw-Hill Education Starting Out with Python (4th Edition)Computer ScienceISBN:9780134444321Author:Tony GaddisPublisher:PEARSON
Starting Out with Python (4th Edition)Computer ScienceISBN:9780134444321Author:Tony GaddisPublisher:PEARSON Digital Fundamentals (11th Edition)Computer ScienceISBN:9780132737968Author:Thomas L. FloydPublisher:PEARSON
Digital Fundamentals (11th Edition)Computer ScienceISBN:9780132737968Author:Thomas L. FloydPublisher:PEARSON C How to Program (8th Edition)Computer ScienceISBN:9780133976892Author:Paul J. Deitel, Harvey DeitelPublisher:PEARSON
C How to Program (8th Edition)Computer ScienceISBN:9780133976892Author:Paul J. Deitel, Harvey DeitelPublisher:PEARSON Database Systems: Design, Implementation, & Manag...Computer ScienceISBN:9781337627900Author:Carlos Coronel, Steven MorrisPublisher:Cengage Learning
Database Systems: Design, Implementation, & Manag...Computer ScienceISBN:9781337627900Author:Carlos Coronel, Steven MorrisPublisher:Cengage Learning Programmable Logic ControllersComputer ScienceISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Programmable Logic ControllersComputer ScienceISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education

Database System Concepts
Computer Science
ISBN:9780078022159
Author:Abraham Silberschatz Professor, Henry F. Korth, S. Sudarshan
Publisher:McGraw-Hill Education

Starting Out with Python (4th Edition)
Computer Science
ISBN:9780134444321
Author:Tony Gaddis
Publisher:PEARSON

Digital Fundamentals (11th Edition)
Computer Science
ISBN:9780132737968
Author:Thomas L. Floyd
Publisher:PEARSON

C How to Program (8th Edition)
Computer Science
ISBN:9780133976892
Author:Paul J. Deitel, Harvey Deitel
Publisher:PEARSON

Database Systems: Design, Implementation, & Manag...
Computer Science
ISBN:9781337627900
Author:Carlos Coronel, Steven Morris
Publisher:Cengage Learning

Programmable Logic Controllers
Computer Science
ISBN:9780073373843
Author:Frank D. Petruzella
Publisher:McGraw-Hill Education