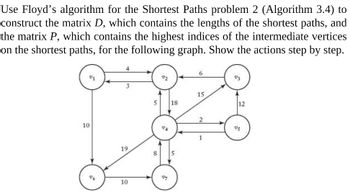
Use Floyd's algorithm for the Shortest Paths problem 2 (Algorithm 3.4) to construct the matrix D, which contains the lengths of the shortest paths, and the matrix P, which contains the highest indices of the intermediate vertices on the shortest paths, for the following graph. Show the actions step by step. 10 4 3 19 10 5 18 8 P 24 6 15 2 1 12 05

Trace Floyd's algorithm for the all-pairs shortest path problem defined over a digraph with vertices V= {1, 2, 3, 4) and whose cost matrix is given below: 11 0482 081 2805 2630 201

I want to learn this. Please explain :)

PROBLEM 6 Part 1. Give the adjacency matrix for the graph G as pictured below: 3 Figure 2: A graph shows 6 vertices and 9 edges. The vertices are 1, 2, 3, 4, 5, and 6, represented by circles. The edges between the vertices are represented by arrous, as follows: 4 to 3; 3 to 2; 2 to 1; 1 to 6; 6 to 2; 3 to 4; 4 to 5; 5 to 6; and a self loop on verter 5.

Consider the un-directed graph shown in the Fig. The values inside the node refer to the feature value of the node. The order of the nodes is A,B,C,D when following the matrix form in below questions.(You can use python or other languages to find the eigen values and other operationfor this question):1. For the given graph, write down the degree matrix, adjacency matrix, and Laplacian matrix representation.2.Find the eigenvalues and eigenvectors of the graph Laplacian matrix. Do you see any pattern pertaining to the signs of the eigenvalues (all positive or negative or no such pattern). Will it be same for all such graph Laplacianmatrices, and why?

Algorithm

Consider the following graph and Dijkstra's algorithm to find the shortest paths from the vertex A.   (See image attached)     The distances / weights in the incident edges at the vertex F are given in the table: edge: (B, F) (C, F) (E, F)distance: 8 11 4.5 At the end of the algorithm, what is the value of the distance for the vertex F?

3. Find a shortest path from node A to node M in the graph with edge weights shown on the graph by Dijkstra's Shortest-Path Algorithm. A 5 3 B 6 1 3 6 2 D 3 2 F 5 2 E 2 3 H 4 3 2 3 4 K 5 M

A.) Running Dijkstra's algorithm with vertex A as the starting point, list the order in which the vertices would be marked. (Don't forget to include the starting vertex.) B.)What is the shortest distance discovered to vertex E? C.In the course of running Dijkstra's algorithm on the graph shown above, how many different (non-infinite) distances were found for vertex E?

Please provide answer fast & It should be correct.