
Concept explainers
Using coding Here you are asked to implement the method by dividing the aperture into a finite
number of segments. Use a unit system where lengths are measured as multiples of
the wavelength of the incident light, λ. Assume that the index of refraction n = 1.00
can be used for air.
Further assume that the horizontal distance between source and aperture X is some
large multiple of λ, and that the same distance is assumed between aperture and
detector screen.
Assume that the aperture size a is some small multiple of the wavelength.
a) Compute the probability amplitude for the central detector height yd = 0 by
using three paths (i) one going directly from source (at height ys = 0, i.e., on the x
axis, via yi = 0 (at the aperture) towards the detector screen;
(ii) then for two straight-line paths: one going via yi = a/2, and one vie yi = −a/2.
The result should be three complex numbers. Show that these are unit-magnitude
complex numbers.
b) Calculate the relative probability for arrival at the detector height y = 0 by
adding the three amplitudes and forming the magnitude squared.
Step by stepSolved in 5 steps with 3 images

adding on to the question:
Now choose the detector height (on one side, i.e., y > 0 or y < 0) that
corresponds to an angle where the first minimum in the intensity pattern is expected.
formula given in the picture below m = 1. Repeat the
computations with three paths as before (passing through yi = 0, and yi = ±a/2),
and obtain the relative arrival probability. What is the intensity ratio compared to
the central detector location yd = 0?
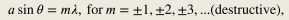
adding on to the question:
Now choose the detector height (on one side, i.e., y > 0 or y < 0) that
corresponds to an angle where the first minimum in the intensity pattern is expected.
formula given in the picture below m = 1. Repeat the
computations with three paths as before (passing through yi = 0, and yi = ±a/2),
and obtain the relative arrival probability. What is the intensity ratio compared to
the central detector location yd = 0?
- Plot (as a function of angular frequency), the magnitude and the phase of the impedance resulting from a resistor (1.2 kOhm) and inductor (1.5 mH) in parallel. Use a logarithmic axis for the frequency, and for the magnitude. Use the range [10, 10**10] rad/s. The impedance of an inductance L is ???Ljω. Label axes. In python and can use cmath if neededarrow_forwardSuppose that you want to calculate 1434661 · 3785648743 − 100020304 · 54300201. You are told thatthe answer is a positive integer less than 90. Compute the answer mod 10 and mod 9, then combineto get the answer. Show all the necessary work to obtain your answers. Note: This technique hasoften been employed to do calculations with large integers because most of the computations use smallintegers, with only the Chinese Remainder Theorem step requiring large integers. For example, if theanswer is known to be less than 1036, the calculations can be done mod p for each prime less than100. Since the product of the primes less than 100 is approximately 2.3 × 1036, the Chinese RemainderTheorem gives the answer exactlyarrow_forwardConsider two traffic lights in a junction that each one has a 7-segment display to show the remaining time. The traffic lights are working as follows: State1: Traffic light 1=GREEN Traffic light 2=RED for 10 seconds,State2: Traffic light 1=YELLOW Traffic light 2=YELLOW for 2 seconds,State3: Traffic light 1=RED Traffic light 2=GREEN for 6 seconds,GOTO State1 During each step, the amount of remaining time should be displayed on the 7-segment and it should be updated every one second. For example in State 1, the display shows 9, then after a second it shows 8, and ... finally, it shows 0 for one second, and the control moves to State 2Write an 8051 assembly program according to the Edsim51 configuration, LED 0, LED1 and LED 2 construct the first traffic light, and LED 3, LED 4, and LED 5 can be used for the 2nd traffic light. Assume that the lookup table for 7segment exists on memory at address 0F00harrow_forward
 Database System ConceptsComputer ScienceISBN:9780078022159Author:Abraham Silberschatz Professor, Henry F. Korth, S. SudarshanPublisher:McGraw-Hill Education
Database System ConceptsComputer ScienceISBN:9780078022159Author:Abraham Silberschatz Professor, Henry F. Korth, S. SudarshanPublisher:McGraw-Hill Education Starting Out with Python (4th Edition)Computer ScienceISBN:9780134444321Author:Tony GaddisPublisher:PEARSON
Starting Out with Python (4th Edition)Computer ScienceISBN:9780134444321Author:Tony GaddisPublisher:PEARSON Digital Fundamentals (11th Edition)Computer ScienceISBN:9780132737968Author:Thomas L. FloydPublisher:PEARSON
Digital Fundamentals (11th Edition)Computer ScienceISBN:9780132737968Author:Thomas L. FloydPublisher:PEARSON C How to Program (8th Edition)Computer ScienceISBN:9780133976892Author:Paul J. Deitel, Harvey DeitelPublisher:PEARSON
C How to Program (8th Edition)Computer ScienceISBN:9780133976892Author:Paul J. Deitel, Harvey DeitelPublisher:PEARSON Database Systems: Design, Implementation, & Manag...Computer ScienceISBN:9781337627900Author:Carlos Coronel, Steven MorrisPublisher:Cengage Learning
Database Systems: Design, Implementation, & Manag...Computer ScienceISBN:9781337627900Author:Carlos Coronel, Steven MorrisPublisher:Cengage Learning Programmable Logic ControllersComputer ScienceISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Programmable Logic ControllersComputer ScienceISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education





