Question
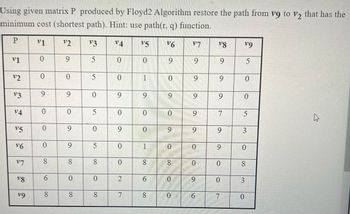
Transcribed Image Text:Using given matrix P produced by Floyd2 Algorithm restore the path from v9 to V2 that has the
minimum cost (shortest path). Hint: use path(r, q) function.
P
v1 "2
V3
v4
V5 V6
V7
8
90
19
v1
0
6
5
0
0
9
22
0
0
5
0
1
0
6
6
9
5
0
6
V3
6
9
0
6
9
9
9
9
0
v4
0
0
5
0
0
15
0
9
0
9
0
9
0
6
6
9
7
5
4.
3
0.
9
8
9
8
V6
17
18
19
8
8
0
0
2
7
8
5
0
1
0
0
9
0
8
0
8
8
0
9
8
0
0
8
9
0
3
0
6
7
0
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 7 steps with 1 images

Knowledge Booster
Similar questions
- Python Help(I need code for Part A)arrow_forwardv1 0 9 0 0 5 0 1 33 9 9 0 9 9 1. Using given matrix P produced by Floyd2 Algorithm restore the path from v3 to 2 that has the minimum cost (shortest path). Hint: use path(r, q) function. P Iv 22 22 ང་ 35 V4 0 50 69 0 6 V7 89 V9 9 5 9 9 0 9 9 0 V4 V5 44 FE 0 0 5 0 0 0 0 9 0 9 0 6 6 6 7 5 9 3 V6 0 9 5 0 1 0 0 9 0 V7 4 8 8 8 0 8 8 ထ 0 0 8 88 6 0 0 2 9 0 9 10 3 v9 8 00 8 8 7 8 0 16 7 7 0arrow_forwardI have spent hours on internet to find an example of iterative lengthening search algorithm but found nothing. I need it ASAP. Can anyone help me? Please. It is its definition: Iterative lengthening search is an iterative analogue of uniform-cost search. The basic idea is to use increasing limits on path cost. If a node is generated whose path cost exceeds the current limit, it is immediately discarded. For each new iteration, the limit is set to the lowest path cost of any node discarded in the previous iteration. I dont understand many things in this definition. 1-What is the first limit before we start? 2-Do we delete the discarded node from the graph or what? 3-What is the generated node? Is it expanded or is it just found as neigbor? 4-What is "lowest path cost of any node discarded"?? Path from where to where?? From start to that node or what? 5-What does path cost mean in this problem? Is it from source to the new node or between current node and next chosen node? I am literally…arrow_forward
- 0 1 0 0 00 0 1 00 1 1 00 00 1 -0 0 1 0 1. 01 0 0.arrow_forward2. Write a function usolve, analogous to function 1solve in section 7.2.2, to solve an upper triangular system Ux = y. [Hint: Loops can be run backwards, say, from n down to 1, by typing in MATLAB: for i=n: - 1:1. Remember also that the diagonal entries in U are not necessarily 1.] I atarrow_forward1.0 1 0 0 00 0 1 00 1 1 00 00 1 -0 0 1 0 1. 01 0 0.vode-Code.arrow_forward
- Let u, v and w be three n-dimensional column vectors. We would like to compute r = uvw, which is also an n-dimensional vector. Justify your answer on which of the following sequence of computation is better: (uv)w_or_u(vw)?arrow_forwardUsing given matrix P produced by Floyd2 Algorithm restore the path from v9 to V2 that has the minimum cost (shortest path). Hint: use path(r, q) function. P v1 "2 V3 v4 V5 V6 V7 8 90 19 v1 0 6 5 0 0 9 22 0 0 5 0 1 0 6 6 9 5 0 6 V3 6 9 0 6 9 9 9 9 0 v4 0 0 5 0 0 15 0 9 0 9 0 9 0 6 6 9 7 5 4. 3 0. 9 8 9 8 V6 17 18 19 8 8 0 0 2 7 8 5 0 1 0 0 9 0 8 0 8 8 0 9 8 0 0 8 9 0 3 0 6 7 0arrow_forwardConsider the following code:> x <- matrix(rnorm(n = 500), ncol = 5)> varx <- var(x)Starting with varx, use two applications of the sweep() function, one dividing each row of the matrix andthe other dividing each column, of a covariance matrix to obtain R, the correlation matrix.arrow_forward
arrow_back_ios
arrow_forward_ios