
Concept explainers
Find the equations for slope and deflection of the beam using direct integration method.
Answer to Problem 6P
For segment AB:
The equation for slope is
The equation for deflection is
For segment BC:
The equation for slope is
The equation for deflection is
Explanation of Solution
Calculation:
Consider flexural rigidity EI of the beam is constant.
Draw the free body diagram of the beam as in Figure (1).
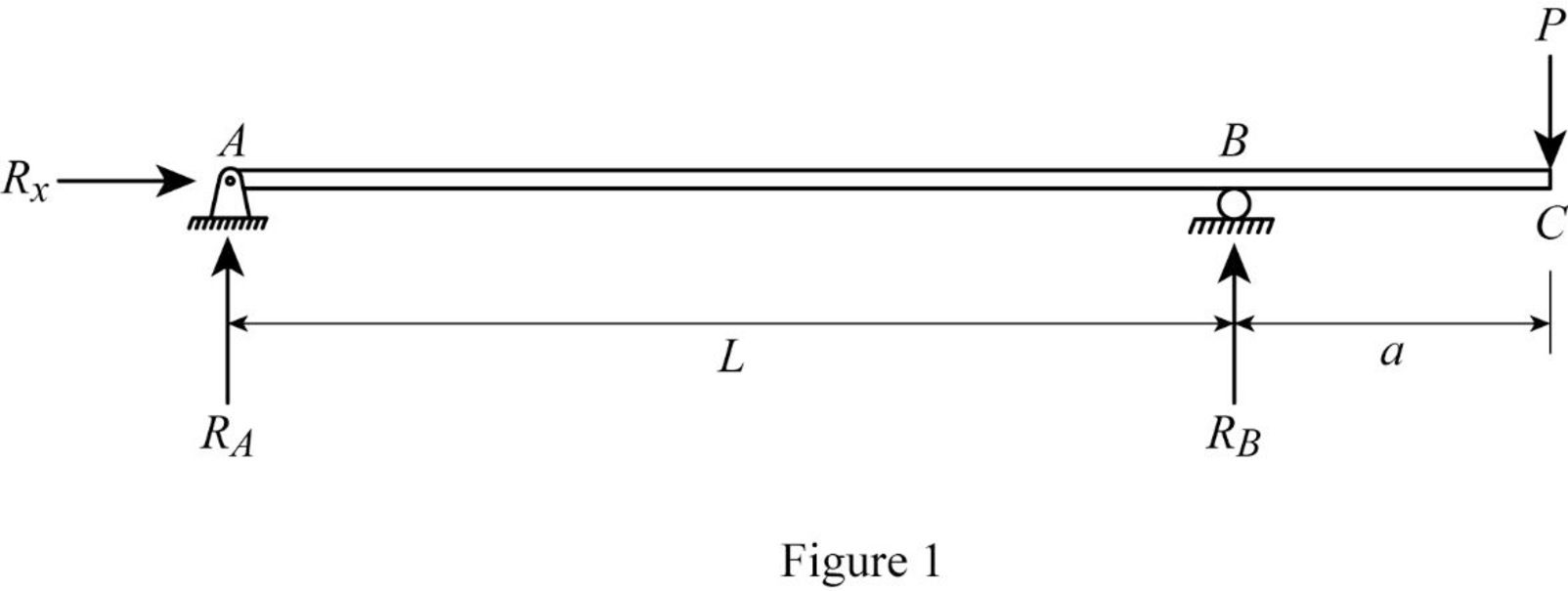
Refer Figure (1),
Consider upward force is positive and downward force is negative.
Consider clockwise is negative and counterclowise is positive.
Determine the support reaction at A using the relation;
Determine the support reaction at B using the relation;
Show the reaction values as in Figure (2).

Take a section at a distance of x.
Show the section as in Figure (2).
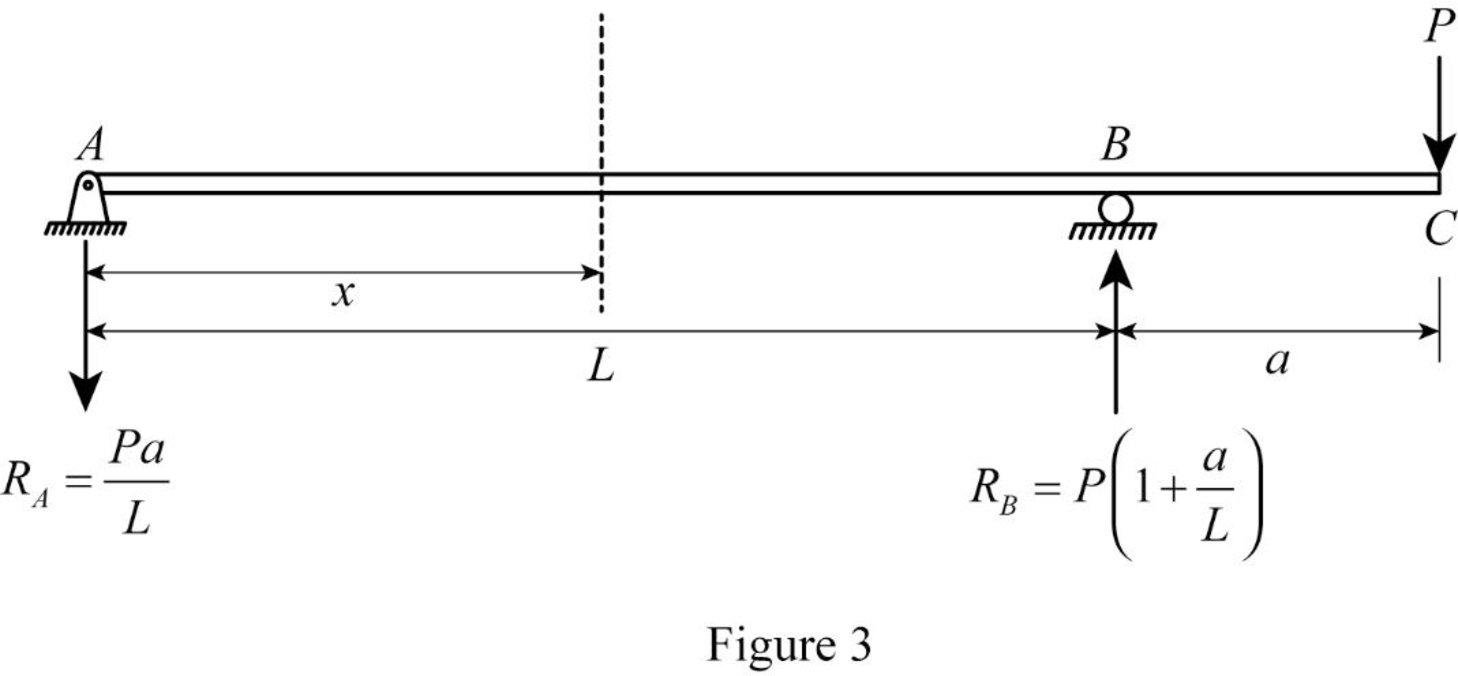
Consider the segment AB:
Refer Figure (2),
Write the equation for bending moment at x distance.
Write the equation for
Write the equation for slope as follows:
Integrate Equation (1) with respect to x.
Write the equation for deflection as follows:
Integrate Equation (2) with respect to x.
Find the integration constants
Write the boundary conditions as follows:
Apply the above boundary conditions in Equation (3):
Write the boundary conditions as follows:
Apply the above boundary conditions in Equation (3):
Find the equation for slope.
Substitute
Thus, the equation for slope is
Find the equation for deflection.
Substitute
Thus, the equation for deflection is
Consider segment BC;
Show the distance at a distance of x as in Figure (4).
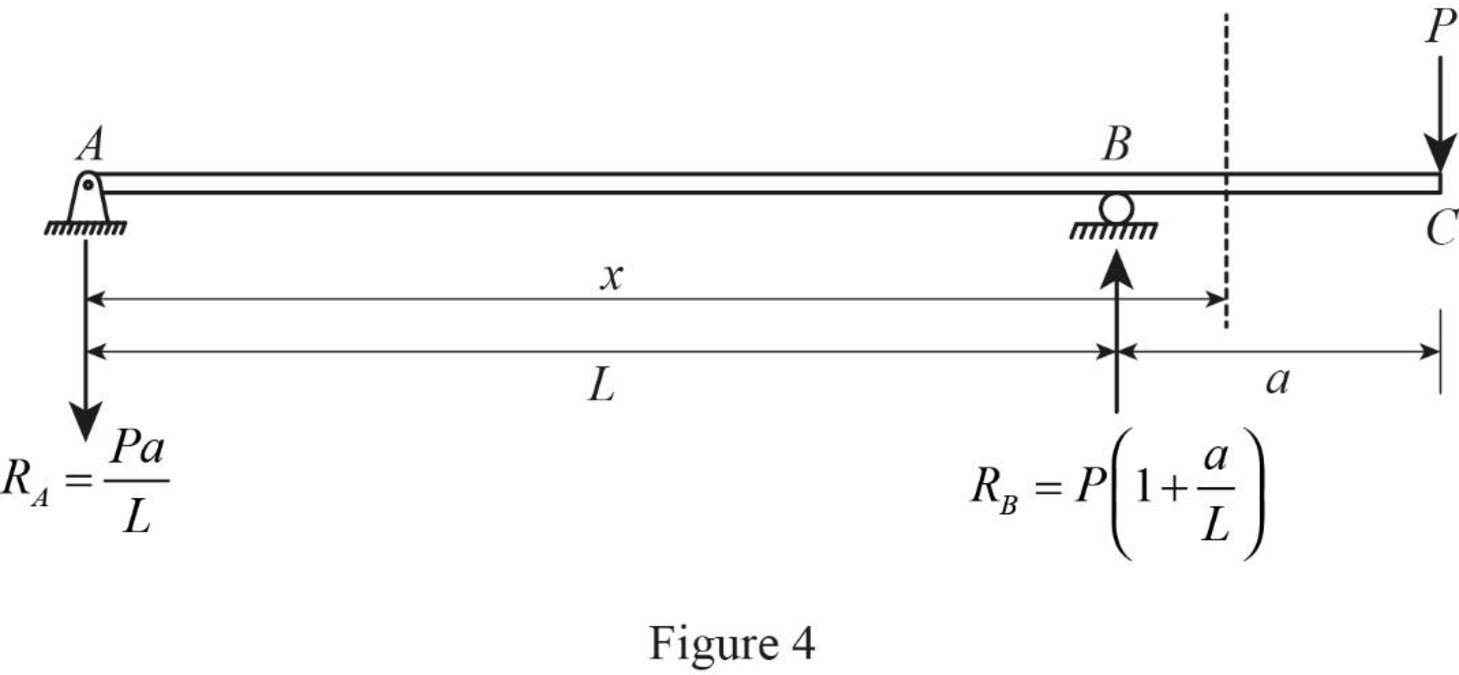
Refer Figure (2),
For segment BC the limit should be
Write the equation for bending moment at x distance.
Write the equation for
Write the equation for slope as follows:
Integrate Equation (4) with respect to x.
Write the equation for deflection as follows:
Integrate Equation (5) with respect to x.
Write the boundary conditions as follows:
The slope at left and right of support B is equal.
Substitute
Apply the above boundary conditions in the above Equation
Substitute
Hence, the Equation for slope is
Write the boundary conditions as follows:
Apply the above boundary conditions in Equation (6):
Substitute
Hence, the Equation for deflection is
Want to see more full solutions like this?
Chapter 6 Solutions
Structural Analysis
