What is Game Theory?
In the current scenario, every market in each part of the world becomes competitive, yet there is some market where there is a lack of competition that gives each firm a higher degree of market power. Yes, you are thinking correctly, it is an Oligopoly market. This form of the market has a fewer number of sellers that dominate the entire industry. There are other unfair market practices related to this market structure like forming a cartel, lack of consumer choice, charging a higher price, restricting the market output, and so on.
Oligopoly Market Structure and Game Theory
One of the branches of the oligopoly market structure is related to the concept of game theory. This branch theoretically shows structure concerning the social situation among competing market players. In general terms, a game theory can be stated as the act of taking independent efficient decision-making among the competing firms (actors) in a specific strategic setting.
Now preceding further will help us to study this interesting topic of game theory in-depth:
Game theory was introduced by Neumann and Morgenstern in 1944 in their work “Theory of Games and Economic Behavior”. The motive behind this development was to find the solution for the problems concerning the bilateral monopoly, duopoly, and oligopoly. In all the above-market structures, a stable and determinate solution is hard to derive as there always exists a conflict between the interest groups, individuals, and firms.
The main aim to study game theory is that each participant of a given game is not dependent on his/her strategy rather the strategy of other participants can also impact their strategy. For instance, like in the case of chess, military battles, and economic markets.
Usually, a game has specified procedures and set rules that two or more market participants have to follow wherein a participant can be stated as a player. Also, a strategy can be depicted as a particular application of the given rules that shows a specific result. Majorly, when a move is made by one player then it will open different ways for opponents to respond and the choice made from all the given responses.
Assumptions of Game Theory
1. The number of players or competitors are finite/limited.
2. All participants acted rationally and intelligently.
3. The rules related to the playing of the game are known to each participant.
4. There is always a conflict between the interests of the participants.
5. Each participant has a finite set of actions.
Nash Equilibrium
Nash equilibrium theory was given by John Nash. Nash was awarded the Nobel Prize in the year 1994 for his contribution to the development of game theory.
Nash theory can be depicted as a decision-making theorem in the game theory that shows the participants in a game can achieve the desired outcome by making themselves stable at the initial strategy.
In this theory, each participant’s optimal action is set after considering the decision of other players. All the participants win as each of them gets the desired outcome. Furthermore, this theory does not necessarily mean that the most optimal strategy of the game is chosen.
Dominant Strategy
A dominant strategy in a game theory can be stated as the theory where from the optimal action for a participant is played from all the available competitive set of actions, irrespective of what other participants or opponents may play.
Mixed Strategy
A mixed strategy in a game theory can be stated as the theory of the probability distribution of a game that one participant chooses randomly among all the given actions set to avoid being predictable. The Nash equilibrium in this kind of strategy can be determined when the given action is best for a participant against the actions that other players use.
Forms of a Game
There are different varieties of the game related to the game theory that each participant plays in the market. Let us start with a strategic game form-
A strategic form in the game theory is a normal way to describe the game by using a matrix wherein each player exhibits itself on each side of the matrix, given the strategies that they will choose, and the set of payoffs related to those strategies that they can receive.
For Example: In the below figure the given matrix shows the same:
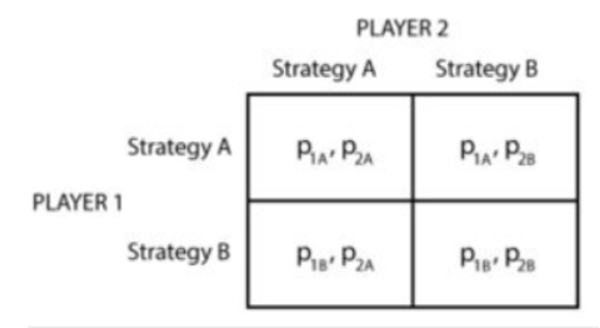
Here, there are two players (1 and 2) and two strategies (A and B). The values given inside the matrix depict payoffs that each player can receive for a given strategy.
Besides this, there are three main games
1. Simultaneous games
2. Sequential games
3. Zero-sum games
Simultaneous Game
A simultaneous game in game theory is one of the kinds of static move games where each player selects their action without knowing the actions of other players/rivals. In this game, each player chooses their playing strategy simultaneously without having any knowledge about their rivals. For learning the simultaneous game as an integral part of the game theory, the most prominent example is the “Prisoner dilemma”.
For Example: In the “Prisoner dilemma” game, two prisoners have to decide whether they will confess a crime or lie about it. In this game, the payoff values are negative as there is imprisonment of the participants. From the beneath matrix, when both participants confess or cooperate then they will go for 8 years in prison, when both participants cooperate and tell lies about it then they will go for 1 year each in prison. But, when one participant confesses and the other lies about it then the participant who confesses will go out of prison while the other has to stay in prison for 10 years. After eliminating the dominant strategy, it can be analyzed that the (Confess, Confess) is the Nash equilibrium.

Sequential Game
A sequential game is also a static form game but is less written in the static form as one player chooses their set of actions or strategies before other players. This game theory has the most positive effect of this first move by one player is that other players have more information regarding the first mover player.
For Example: Let us look at a case where player 1 has two strategies Up and Down (U/D) and player 2 has to decide between going Left or Right (L/R). So, we can estimate this game by using the strategic form by giving all the possibilities for player 2-
1. Go R if player 1 goes U, otherwise, go L.
2. Go L if player 2 goes U, otherwise, go R.
3. Go R, no matter what.
4. Go L, no matter what.
Solution : Now, this game can be written using the extensive form of the strategic form. Below images depict the same:
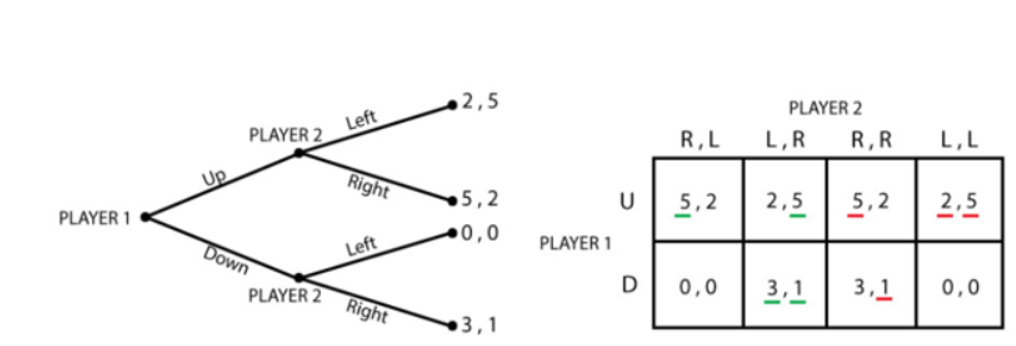
In this case, the green color depicts the perfect subgame Nash equilibrium, and the red color depicts the subgame imperfect Nash equilibrium.
Zero-Sum Game
A game is categorized as a zero-sum game when the loss of one participant exactly matches the gain of another participant making the net change in the wealth zero. Usually, this game can include either only two participants or millions of participants. Generally, future and options are an example of this. Also, most of the transactions can be depicted as a non-zero-sum game as the end outcome can be beneficial for both participants.
Limitations of Game Theory
- Many businesses do not have fewer competitors but infinite so as the number of participants rises in the real business environment becomes more difficult.
- In a broader sense, it gives a general rule of logic for operating in a market rather than defining a winning strategy for the market participants.
- The real-life business operating environment is full of uncertainty so it cannot be depicted and considered in a game theory.
- Game theory is based on the assumption of rationality and utility maximization wherein individuals in real life do not sacrifice for themselves for the betterment of society.
- Lastly, most importantly the businessmen do not have adequate knowledge regarding the game theory.
Context and Applications
Many economists and scholars state that the game theory can be used to decide the optimal outcome when a conflicting situation arises so there are ample possibilities for this branch in running a successful business in a competitive market. Computers also play a crucial role as they help to study the impact of a large number of independent variables of the market with mathematical accuracy. There are many benefits of using game theory in practical lifelike-
- Game theory gives a systematic quantitative approach for determining the optimal strategy in the competitive business environment.
- Game theory gives a dummy for the competitors’ reaction to the firm’s action.
- In competitive situations, this theory helps in handling the independence of firms from each other.
- This theory helps in making rational decisions by truly acting as a management device.
In the present scenario, the markets tend to be highly competitive due to the existence of fair market practices and different trade laws so there is a large scope of studying game theory. Even today, many economists pursue their higher studies (Ph.D.) in this which makes it an interesting area for different students.
Related Concepts
- Game - it is the set of circumstances whose result is dependent on the actions of other decision-makers.
- Strategy - it is a full plan of the action of a player that a player can play in a given set of circumstances that arise from within the game.
- Payoffs - it is the sum of money/utility that a player receives from playing.
- Players - they are the decision-maker whose use a different set of strategies to play a game.
- Equilibrium - it is the point of the game where all the players have made their decisions and the optimal outcome is reached.
Practice Problem
1. Consider the below example of a zero-sum game and find the best outcome:

Solution:
The given matching pennies game is a zero-sum game as in this case, the gain of one player is the loss for the other player. As shown in the above payoff matrix, the combined payoff of players A and B in all four cells is zero.
2. Consider the below case of the Prisoner dilemma where there are two players A and B. Both players can remain silent (S), confess (C), and choose between S or C. find the Nash equilibrium?
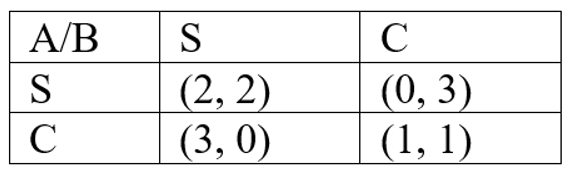
Solution:
Generally, it is optimal for both players A and B to remain silent, but it is not likely to happen because C strictly dominates the move S. Thus, it can be noted that the best response to S is C and C is to C. Hence, the pair (C, C) is the unique Nash equilibrium of the game.
Want more help with your economics homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Game Theory Homework Questions from Fellow Students
Browse our recently answered Game Theory homework questions.