What is the Theory of Production?
Production is the process by which goods and commodities are produced for selling in the market, and for consumption by the individuals. In terms of economics, when inputs (raw materials) are converted into outputs (finished goods), it is called production. Theory of Production is the study that helps in understanding the relationship between inputs and output.
This theory of production is propounded by Tjalling Koopmans, who was a Dutch American economist and mathematician. Consider an example about the production of a chair. For manufacturing a chair, what are the basic inputs required? (For the fact of simplicity, considering the basic raw materials required to produce chairs). It will definitely need a log of wood or simply wood. Here, wood is the input of raw material, and the chair which is made out of the wood is considered to be the output. Therefore, the relation between the chair and log of wood is the theory of production. Therefore, a log of wood will not be of any use to anyone, but a chair will be useful for the purpose of sitting on it. Thus, production is not only creating goods and services but also adding usefulness or utility to output. Production not only includes the creation of physical goods but also various services like services provided by doctors or teachers or lawyers, etc.
What is Cost Theory?

Theory of Production provides the base of “theory of cost”. By the theory of cost, we mean the relation between the cost and the output. Now the question is, what is the cost? Cost is the expense that is incurred by the producer for carrying out the production process.
For example. For carrying out a production process, there are various factors, like labor, land, capital (loan) (and entrepreneur, which are collectively called factors of production). Now, these factors of production require a cost to operate like labor requires wages to operate, capital requires interest rate and land requires rent. Therefore, these are included within the cost.
What is Production Function?
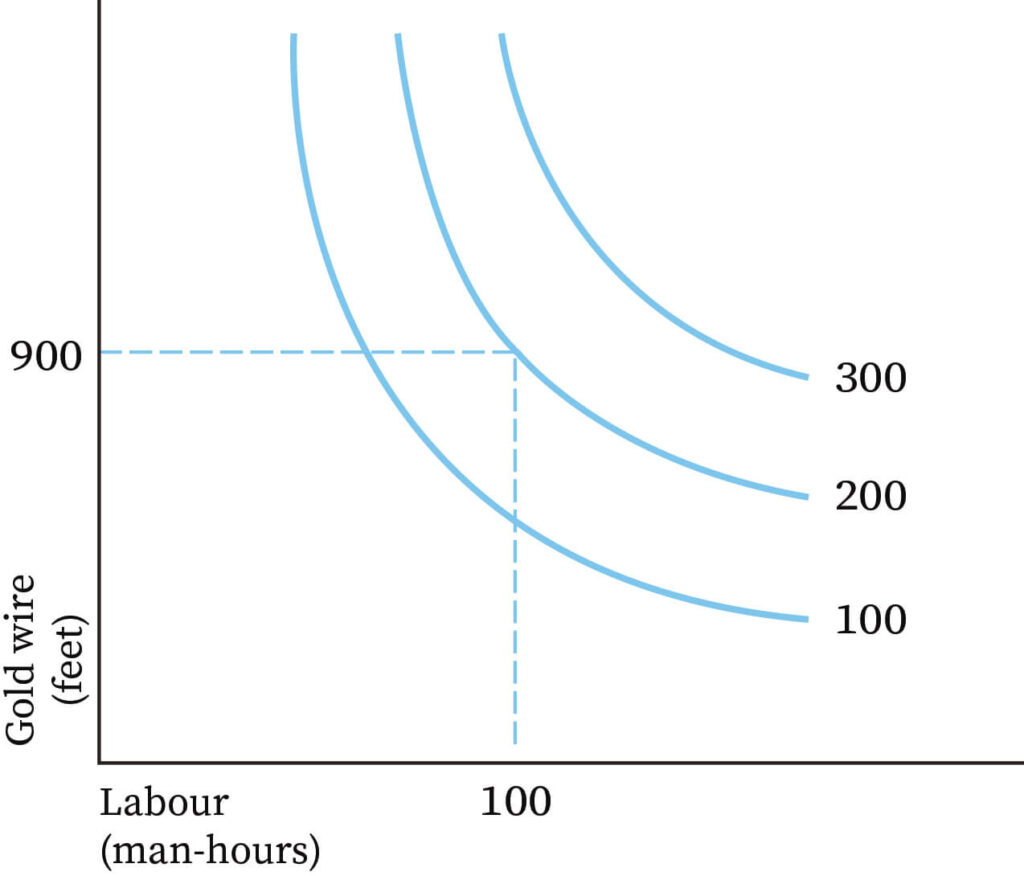
From the point of view of economics, we have already seen that the production process includes the use of various kinds of factors of production. This can be understood with the help of an example. The production function for a shoe making factory may indicate that maximum quantity of shoes can be produced per day with a given amount of leather, glue, labor machinery, etc. If this is seen from another way round, the production function for shoe production factories comprises minimum quantities of glue, leather, labor, machinery, etc. required to produce a certain number of shoes, say 50 pairs, per day. In the form of an algebraic equation, the production function for a commodity or good can be expressed as:
Qx = f (f1, f2, f3, …….. fn)
Where Qx is the quantity of output of commodity X, and f1,f2, f3,……..fn are the number of different inputs used to produce Commodity X. To understand this in a simpler way, we will assume that there are only two inputs, specifically, labor (L), and capital (K), then the production function will be:
Qx = f(L, K)
In the above production function, the quantity of Commodity X produced is the function, that is, depended on the quantity, L and K.
In economic theory we basically refer to two types of production functions:
- Short-run production function: It refers to a situation when only one input is the variable, and all the other inputs are assumed to be the constant. In this case, we will do the analysis of the effect of change in the quantity of one input on total output by keeping all the other inputs unchanged. At any point in time, there is certain capital stock, a set of machines. If more workers are employed on these given factors of production to get more output, the relation between the variable input (labor) and output is known as the short-run production function.
- Long-run production function: It refers to a situation when all the inputs are variables which can be changed or altered by increasing or decreasing in the same proportion. The long-run production function does the analysis of changes in output when all inputs used in the production process of a commodity are changed simultaneously and in the same proportion.
Returns to a Factor and Returns to Scale
The effect on output when only one input is changed and the other factors remain constant, is termed as the Returns to a Factor. It refers to the effect on total production when both or all the inputs are altered, which is known as returns to scale. Let us understand this with the help of an example:
In an economy, there is a firm and it uses inputs in the following manner:
| Inputs(units) | Output(units) |
| 1 Capital + 1 Labor | 100 |
| 2 Capital + 2 Labor | 200 |
By using 1 unit of labor (L) and 1 unit of capital (K), the output that is produced in the economy is 100 units of output. This means that increase in the outcome is at the same rate as increase in quantity of all inputs, this is known as constant return to scale. Algebraically, it would look like:
100Q= f (1L, 1K)
200Q= f (2L. 2K)
In an economy, there is a firm and it uses inputs in the following manner:
| Inputs(units) | Output(units) |
| 1 Capital + 1 Labor | 100 |
| 2 Capital + 2 Labor | 250 |
In this case, we get to see that even when the inputs are increased in the same rate or proportion, the total outcome increases more than its proportion. This is known as increasing returns to scale.
In an economy, there is a firm and it uses inputs in the following manner:
| Inputs(units) | Output(units) |
| 1 Capital + 1 Labor | 100 |
| 2 Capital + 2 Labor | 150 |
On the other hand, we get to see here that, though inputs are increased, the total outcome is increased but at a diminishing rate as compared to previous cases.
Formulas
Total Product (TP) is the total amount of goods produced during a certain time with the combination of a certain amount of variable factor and fixed factors. Average Product (AP) is the product that is being produced by each variable factor. Marginal Product (MP) refers to a change in the total product due an increase in input (variable input) by an additional unit.
- Production Function: Qx = f (L, K)
- Average Product: APL = TPL /L
- Marginal Product: MP = DTP/DL
- MPnth = TPn – TPn-1
Total cost is the cost that is incurred for producing total product.
Average cost is the cost of per unit of product produce of both the fixed and variable factors of production.
Marginal cost is the addition that is made to the total cost for producing one more unit of the output.
Application
It will be easier to understand the above-mentioned concepts with the help of the following table:
| No. of Workers (L) | Total Product (TP) | Average Product (AP) | Marginal Product (MP) |
| 0 | - | - | - |
| 1 | 100 | 100 | 100 |
| 2 | 220 | 110 | 120 |
| 3 | 360 | 120 | 140 |
| 4 | 520 | 130 | 160 |
| 5 | 650 | 130 | 130 |
| 6 | 750 | 125 | 100 |
| 7 | 840 | 120 | 90 |
| 8 | 880 | 110 | 40 |
| 9 | 880 | 97.7 | 0 |
| 10 | 830 | 83 | -50 |
| 11 | 770 | 77 | -60 |
The above table gives us the following results:
- When MP>AP, it means that AP is rising. This is the case of up to 4 units of labor. Hence, we can say that, if an additional worker is to increase the average product of all the workers, the MP of the additional worker must be greater than the average product of the existing worker.
- When MP=AP, it means that AP is constant. This happened when 5 workers were employed.
- When MP<AP, it means that AP is falling. In our example, it begins when the 6th worker is employed.
- When TP increases at an increasing rate, MP increases. TP increases at an increasing rate up to the employment of 4 workers. Hence in this range MP is also increasing.
- While TP increases at a diminishing rate, MP declines. This happens in the range of employment of 5 workers to 8 workers. Here, MP is also decreasing.
- When TP reaches maximum, MP becomes 0. Here, it occurs with the employment of 9 workers.
- When TP begins to decline. MP becomes negative. This occurs from the employment of 10 workers onwards.
Practice Problem
Question 1)
Calculate the AP and MP.
| Units of labor input | 1 | 2 | 3 | 4 | 5 | 6 |
| Total Output (Units) | 50 | 110 | 150 | 180 | 180 | 150 |
Question 2)
Define Production Function.
Question 3)
Answer the following question in short:
- When MP=0, what is the level of TP?
- When MP is negative, what happens to TP?
- When AP is constant, what is the relation between MP and AP?
Question 5) What is the difference between Short-run and Long-run production function?
Context and Applications
The production decisions are taken by the owner based on what kind of profit is expected. As because for any company or business profit making is the sole purpose.
This topic is significant in the professional exams for both undergraduate and graduate courses, especially for
- B.Sc. in Economics
- M.Sc. in Economics
Want more help with your economics homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Theory of Production Homework Questions from Fellow Students
Browse our recently answered Theory of Production homework questions.