What is a curve?

A curve is a turn that is provided horizontally or vertically in the design of highways, railways, and runways. A curve connects two straight lines that are separated by the deflection angle. It helps to change the direction and alignment of the highways, railway tracks, and runways. Therefore, the gradual change in their alignment is made by using a curve to provide comfort to the passengers and this also provides an easy turn to change the direction of the moving vehicle.

Horizontal curve

This is the type of curve that provides a change in the direction of the road with respect to its centerline. When a vehicle moves on the horizontal curve, it experiences a centrifugal force that acts outwards through its center of gravity. This centrifugal force is dependent on the radius of the horizontal curve and the speed of the vehicle. This force can be overcome by the frictional force that is developed between the types of vehicles and the pavement. Therefore, the centrifugal force ‘P’ can be calculated by using the equation-

$P=\frac{W{v}^2}{gR}$

Where

$W$= Weight of the vehicle,

$v$= Speed of the vehicle

$g$= Acceleration due to gravity

$R$= Radius of the curve

Design of horizontal curve

Super elevation

A super elevation is provided to counteract the centrifugal force and to reduce the chances of the vehicle skid or overturning. The outer edge of the pavement is raised with respect to the inner edge of the pavement. A super elevation is a transverse slope throughout the entire length of the curve. 

The general equation for the design of super elevation ‘e’ is given as-

$e+f=\frac{V^2}{127R}$

Where

$f$= The coefficient of lateral friction. It has a value of 0.15

$V$= Speed of the vehicle in kmph

$R$= Radius of the curve in meters

Radius of horizontal curve

The horizontal curve should be effectively designed by considering the specified designed speed of the highway. The radius should be kept high to maintain the centrifugal ratio within its low limit. 

The minimum radius of the horizontal curve ‘$R_{ruling}$’ can be calculated by using the relation-

 $R_{ruling}=\frac{V^2}{127(e+f)}$

Widening of pavement on a horizontal curve

The pavement is slightly widened more than the normal width on the horizontal curve for off-tracking, to enhance visibility and to overtake the vehicles with greater clearance.  The extra widening of the pavement is classified into two categories- mechanical widening and psychological widening. 

Mechanical widening

This is the extra widening provided for off-tracking due to the rigidity of the wheelbase. The mechanical widening ‘$W_m$’ is given as-

$W_m=\frac{n{l}^2}{2R}$

Where

$n$= Number of traffic lanes

$l$= Length of the wheelbase

$R$= Mean radius of the horizontal curve

Psychological widening

This is the extra widening provided to maintain greater clearance while overtaking the vehicle. The psychological widening ‘$W_{ps}$’ is given as-

$W_{ps}=\frac{V}{9.5\sqrt{R}}$

The total extra widening is given as-

$W_e=W_m+W_{ps}$

$W_e=\frac{n{l}^2}{2R}+\frac{V}{9.5\sqrt{R}}$

Transition curve

A transition curve is defined as the curve whose radius decreases from infinity at the tangent point to a required designed radius of the circular curve. It is provided between the straight and circular curve and the radius is minimum at the start of the circular curve. It helps to avoid a sudden jerk on the moving vehicle, enables the driver to turn the vehicle with safety, and improves the aesthetic appearance of the highway and the road. The transition curve is further classified into three types:

1. Spiral Transition Curve: The radius is inversely proportional to the length of the curve. The rate of centrifugal acceleration is uniform throughout the length of the curve. This is the ideal transition curve.
2. Lemniscate Transition Curve: The rate of centrifugal acceleration is not uniform throughout the length of the curve at a deflection angle of more than $4°$.
3. Cubic Parabola Transition Curve: The rate of centrifugal acceleration is not uniform throughout the length of the curve at a deflection angle of more than $4°$.

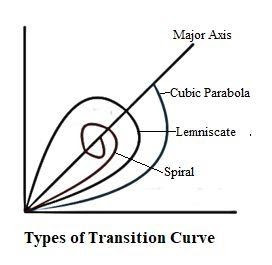
Design of transition curve

The length of the transition curve is obtained by developing the

Rate of change of centrifugal acceleration

The centrifugal acceleration should be designed to the lowest rate so as to not cause discomfort to the travelers that are moving at a design speed ‘v’ in m/sec.

The length of the transition curve '$L_s$' can be obtained by the equation- 

$L_s=\frac{0.0215V^3}{CR}$

Where

$V$= Design speed in kmph

$C$= Allowable rate of change of centrifugal acceleration. Its value varies from 0.5 to 0.8 $m/s^3$.

$R$= Radius of the circular curve

Rate of super elevation

It is not desirable to raise the outer edge of the pavement at a higher rate than 1 in 150 with respect to the grade of the centerline. The length of the transition curve should be at least 150 times the total amount of the raise of the outer edge of the pavement.

If the pavement is rotated about the centerline, then the length of the transition curve is given as-

$L_s=\frac{eN}{2}(W+W_e)$

If the pavement is rotated about the inner edge of the pavement, then the length of the transition curve is given as-

$L_s=eN(W+W_e)$

According to the empirical formula by IRC

• For plain and rolling terrain

$L_s=\frac{2.7V^2}{R}$

• For mountainous and steep terrain

$L_s=\frac{V^2}{R}$

• Setting out of the transition curve

The shift ‘S’ of the transition curve is obtained by the equation-

$S=\frac{{L^2}_s}{24R}$

Where

$L_s$= Length of the transition curve

$R$= Radius of the circular curve

Vertical curve

A vertical curve is introduced at the intersection of the different gradients on the highway for the easy vertical profile of the pavement and to provide easy changes in the gradients for the travelers. A vertical curve is classified into two categories based on the shape of the profile.

Summit curves

They are also called crest curves with the convexity upwards. The deviation angle, N, for the summit curve is the difference of the intersecting gradients.

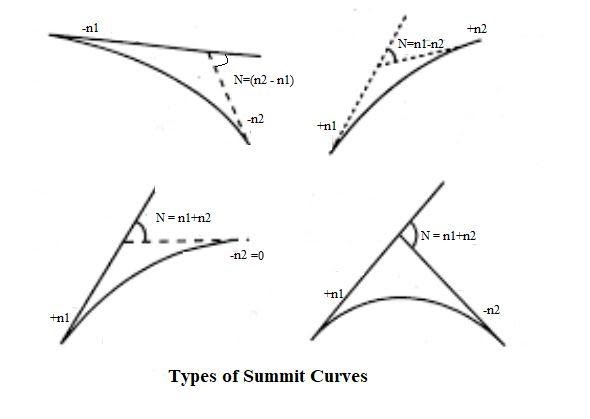
Design of Summit Curve

Length of the summit curve

The length of the parabolic summit curves can be obtained by the given equation-

$y=a{x}^2$

Where

$a$= A constant with the value of $\frac{N}{2L}$

$N$= Deviation angle

$L$= Length of the summit curve

Length of the summit curve for Stopping Sight Distance (SSD)

Case I: When L > SSD

$L=\frac{N{S}^2}{(\sqrt{2H} +{\sqrt{2h)}}^2}$

Where

$N$= Deviation angle

$S$= Stopping Sight Distance (SSD)

$H$= Height of the eye level of the driver above the roadway 

$h$= Height of the subject above the pavement

This equation can be modified by substituting the values of H as 1.2 m and h as 0.15 m as per the IRC Standards.

∴ $L=\frac{N{S}^2}{4.4}$

Case II: When L < SSD

$L=2S-\frac{(\sqrt{2H}+{\sqrt{2h)}}^2}{N}$

This equation can be modified by substituting the values of H as 1.2 m and h as 0.15 m as per the IRC Standards.

∴ $L=2S-\frac{4.4}{N}$

Valley curves

They are also called sag curves with the convexity downwards. The deviation angle, N, for the valley curve is the difference of the intersecting gradients.

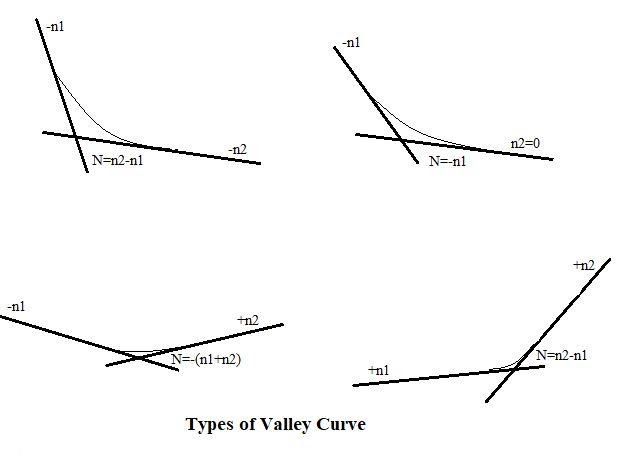
Design of valley curve

The length of the valley curve for comfort condition

The length of the valley curve for comfort conditions can be obtained by allowing the allowable rate of change of centrifugal acceleration.

$L=2\sqrt{\frac{N{v}^3}{C}}=0.38\sqrt{N{v}^3}$

Where

$N$= Deviation angle

$v$= Design Speed in m/sec

$V$= Design Speed in kmph

$C$= Allowable rate of change of centrifugal acceleration

The length of the summit curve for Headlight Sight Distance (HSD)

Case I:  L > SSD

$L=\frac{N{S}^2}{(1.5+0.35S)}$

Case II:  L < SSD

$L=2S-\frac{(1.5+0.35S)}{N}$

Context and Applications

This topic is important for both undergraduate and postgraduate studies in the field of-

• Bachelors in Technology (Transportation Engineering)
• Masters in Technology (Transportation Engineering)

Practice Problems

1. What is the correct equation for the super elevation on the horizontal curve?

1. $e+f=\frac{V^2}{127R}$
2. $e+f=\frac{R{V}^2}{127}$
3. $e-f=\frac{V^2}{125R}$
4. $e-f=\frac{R{V}^2}{125}$

Answer: Option a 

Explanation: The super elevation can be calculated by using the equation $e+f=\frac{V^2}{127R}$

2. What is the design value of ‘f’ in the equation to calculate the super elevation?

1. 0.50
2. 0.45
3. 0.15
4. 0.05

Answer: Option c 

Explanation: The design value for the lateral friction coefficient is 0.15 as per IRC.

3. If the ascending gradient is 1 in 50 and the deviation angle is 1 in 75, then find the ascending gradient.

1. 1 in 40
2. 1 in 20
3. 1 in 30
4. 1 in 10

Answer: Option c 

Explanation: The deviation angle $N=n_2-n_1$

$$\begin{gathered} \frac{1}{75}=n_1-\frac{1}{50} \\ {n}_1=\frac{1}{75}+\frac{1}{50}=\frac{2+3}{150}=\frac{5}{150}=\frac{1}{30} \end{gathered}$$

Therefore, the ascending gradient is 1 in 30.

4. Which factor affects the length of the valley curve?

1. f
2. N
3. V 
4. R 

Answer: Option b

Explanation: The deviation angle N, affects the length of the valley curve.

5. What is the value of the ruling radius for the NH road on mountainous terrain?

1. 50
2. 60
3. 70
4. 80

Answer: Option d

Explanation: The value of the ruling radius for the NH road on mountainous terrain is 80 m as per the IRC standard.