What is Finite Element Analysis?

Finite element analysis (FEA) is a simulating process of the manner and assembly of an object under obtained conditions. It is used for assessing the finite element method (FEM) which includes one or more solution algorithms. General problem areas of interest are structures, heat transfer, the flow of fluid, transport, and some boundary value problems.

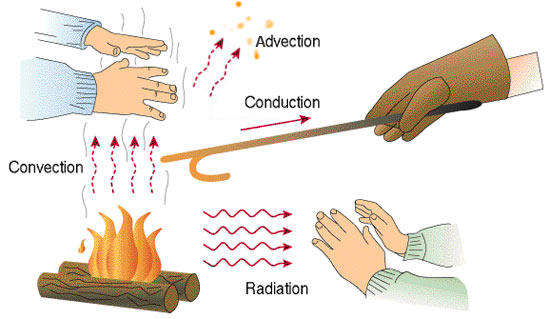
Thermal analysis with finite element analysis permits for resolving the heat transfer in or between solids. Heat transfer categories such as convection, conduction, and thermal radiation can be estimated.

Finite Element Method (FEM) is like a theory manual, with plenty of equations and mathematics. It is usually used for the application of FEM, to solve real engineering problems. Finite element analysis (FEA) software is a computational method for forecasting the reaction of the product.

Heat transfer

Conduction: It is the transfer of heat through solid objects without the bulk motion of the matter.

Convection: The process of heat transfer by the bulk movement of molecules within fluids is called convection. The motion of fluid increases the heat transfer and it is the dominant form of heat transfer in liquids and gases.

Thermal radiation: Radiative heat transfer is the transfer of energy via thermal radiation, electromagnetic waves, and so on.

Heat transfer problems are of critical importance in almost all areas of science, technology, engineering, and management (STEM), especially in the mechanical engineering branch. Various heat transfer problems are assisted by mass transfer.

Concepts of FEM

Workout of FEM

1. Separating the problem domain into sub-domains, with each representing a set of element equations to the original problem.
2. Methodically gathering all the sets of element equations into a globalized system of equations for the ultimate calculation.

The global system of equations can be calculated from the previous values of the original problem to obtain a numerical answer. Element equations are simple equations that determine the original complex equations, where the original equations are often partial differential equations (PDE). Approximation of the PDE locally with a set of algebraic equations for steady-state problems and a set of ordinary DE for transient problems. These equation sets are the element equations. Algebraic equation sets that come from the steady-state problems are evaluated using numerical linear algebra methods, while ordinary DE sets that come from the transient problems are computed by numerical integration.

Application of FEA includes solving complex problems like Euler Bernoulli beam equation, heat equation, Navier stokes equation, and integral equations.

Various types of Finite Element Methods

• Applied Element Method (AEM)
• Augmented Finite Element Method (A – FEM)
• Generalized Finite Element Method: The efficiency of GFEM is seen when applied to problems with domains having complex boundaries, problems with micro-scales, and problems with boundary layers.
• Mixed Finite Element Method
• Variable – polynomial (hp – Finite Element Method) (hp – FEM)
• Hpk – Finite Element Method
• Extended Finite Element Method (XFEM)
• Scaled boundary Finite Element Method (SBFEM)
• Smoothed Finite Element Methods
• Spectral Finite Element Method
• Crystal plasticity Finite Element Method (CPFEM)

Heat conduction analysis

Heat transfer problems include temperature (scaler), heat flux (vector), fixed temperature boundary conditions, heat flux boundary conditions, internal heat generation, and thermal conductivity. Increase in the complex problem level in coupled structural-thermal problems and radiation problems.

The thermal problem’s goal is to solve for temperature distribution for a certain thermal load. The boundary conditions are specified temperature (essential) and specified heat flux (natural).

[K_T] {T} = {Q}

Where,

K_T = conductivity matrix

T = nodal temperature

Q = thermal load

Steady-state heat transfer problem

Fourier heat conduction equation

The flow of heat from the higher temperature to the lower temperature.

$q_x=-kA\left(\frac{dT}{dx}\right)$

where,

kA = thermal conductivity (W/m/ degree Celsius)

q_x = heat flux (watts)

Governing differential equation

1. Conservation of energy

Energy (inside) + Energy produced = Energy (outside) + Energy increase

• Two modes of heat transfer through the body

The prescribed surface flow of heat Qs per unit of area, convective heat transfer, and convection coefficient energy.

• Conservation of energy in steady-state

Delta U = 0 means there is no change in internal energy

$q_x+Q_{s}P\Delta x+h(T^{\infty }-T)P\Delta x+Q_{g}A\Delta x=\left(q_x+\frac{d{q}_x}{d_x}\Delta x\right)$

• Applying Fourier law,

The change rate of heat flux = heat generated + heat transfer

$\frac{d}{dx}\left(kA\frac{dT}{dx}\right)+Q_{g}A+hP\left(T^{\infty }-T\right)+Q_{s}P=0$ and $0\le x\le L$

• Boundary conditions

The prescribed temperature at the boundary (essential) and prescribed heat flux (natural).

Direct method heat conduction

Element equation

• Fourier law of heat conduction
• From the conservation of energy for the element
• on combining the two equations, we get

$\left\{\frac{q_i^{\left(e\right)}}{q_j^{\left(e\right)}}\right\}=\frac{kA}{L^{\left(e\right)}}\left[\begin{array}{cc}1& -1\\ -1& 1\end{array}\right]\left\{\frac{T_i}{T_j}\right\}$

Assembly

• Assembly using heat conservation at nodes

Make a note that heat flow inside the element is positive and similar to the assembly procedure with 1D bar elements.

• Applying BC,

Striking of rows can be worked out but not column striking since prescribed temperatures are not generally zero.

Galerkin method for heat conduction

The direct method is limited to nodal heat input. It requires a better-advanced method for heat generation and heat transfer through convection. Steps include considering an element ‘e’, using interpolation where temperature varies linearly, the heat flux equation where the flow of heat is constant.

Convection boundary conditions

• Convection boundary conditions

This occurs when a structure is surrounded by fluid and is not there in structural problems. The boundary conditions include unknown temperature (mixed) and heat flow not prescribed.

• 1-D finite element: both nodes are along the convection boundary

Convection along the rod: a long rod is submerged into a liquid; convection occurs across the entire surface and governing differential equation is used.

Another example is the heat flow in a cooling fin.

Context and Application

The topic is extensively taught in various undergraduate and postgraduate degree courses like-

• Bachelor of Technology (Mechanical Engineering)
• Bachelor of Technology (Civil Engineering)
• Masters of Technology (FEA Computational Engineering)

Practice Problems

Q1. What is the transfer of heat through liquids and gases called?

1. Conduction
2. Convection
3. Radiation
4. None of these

Correct Option- b

Explanation: The transfer of heat through liquids and gases is called convection

Q2. Which of the following are the types of finite element method (FEM)?

1. Mixed Finite Element Method
2. Variable – polynomial
3. (A – FEM)
4. All of these

Correct Option- d

Explanation: The types of FEM are Mixed Finite Element Method, Variable – polynomial, and (A – FEM).

Q3. What does ‘Q’ mean in the heat conduction analysis equation?

1. Conductivity matrix
2. Nodal temperature
3. Thermal load
4. Rate of flux

Correct Option- c

Explanation: ‘Q’ means thermal load in the heat conduction analysis equation.

Q4. What is the full form of FEA?

1. Finite Element Analysis
2. Finite Element Method
3. Former Element Analysis
4. Finite Addition Method

Correct Option- a

Explanation: Full form of FEA is Finite Element Analysis

Q5. Between what does the thermal analysis conduct heat transfer?

1. Liquids
2. Coefficients of temperature
3. Solids
4. None of these

Correct Option- c

Explanation: Thermal analysis conducts heat transfer between solids.

Related Concepts

• Computational and Numerical Analysis
• Numerical solution algorithm
• Finite element solution
• Numerical modeling