What are loads and reactive forces?
Loads are the external influences that a beam experiences under its working conditions. For instance, a beam may be subjected to shear loads, twisting loads, bending moment, and axial loads during its working conditions. Engineers primarily deal with beams and trusses in the civil engineering domain. Due to the influence of loads, it is very crucial to determine the induced stresses and deformation values. These values give an insight into the critical area of the beam that needs to be worked upon to make it fail-safe.
Due to the application of loads, reactions are induced in the beam, the reactive forces are primarily due to Newton's third law of motion. For calculations, estimation of reactive forces is the first step toward the solution approach. Based on the loading conditions, their different solutions approach.
Simply supported beams
The two extreme ends of the beam always remain supported. One of the support is fixed support where the beam remains pivoted to the support with a hinge, while the other is usually roller support with the end fixed to support by a hinge. The intention of providing the rollers is to take care of the thermal expansion. The fixed support of the beam provides one degree of freedom to the beam, that is, the beam can rotate either clockwise or counter-clockwise, and the roller support provides two degrees of freedom to the beam, that is, the beam can slide horizontally and can also rotate. These supports induce reaction forces to the beam when external forces act on the beam. When vertical forces act on the beam, the fixed support and the roller support will both produce vertical reaction forces. Due to external reaction forces, the fixed support will provide axial reaction forces. A simply supported beam can also be under the influence of distributed loads, these loads instead of acting at a point, remain distributed throughout the length of the beam. To analyze such beams under the effect of distributed loads, a resultant force needs to be determined
Cantilever beams
In these kinds of beams, one end always remains free of any support while the other end remains fixed to a horizontal support. The beam can be subjected to axial loads, shear loads, bending moments, and twisting moments. Under the application of vertical external forces, the beam experiences upward reaction forces along with a bending moment at the fixed end. To determine the bending moment, first, the reaction forces need to be determined.
Over hanged beams
In over-hanging beams, one of the ends of the beam remains extended away from the supports. Such kinds of beams are primarily indeterminate and need additional compatibility equations along with the equilibrium equations to solve for the reactions and unknown loads. One of the ends remains pivoted, while the other ends remain roller supported. The loading conditions of an over-hanged beam can be either static point loads or may be uniformly distributed or uniformly varying loads.
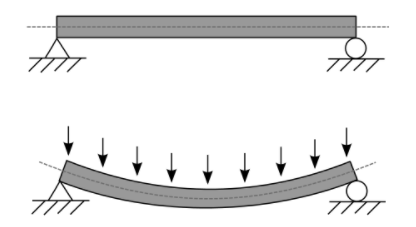
Analysis of beams
Analysis of beams requires determining the unknown forces, reactions, and moments. A beam is assumed to be in equilibrium under the influence of such loads, that is, the inertia of the beam at rest is considered. Laws of equilibrium are then applied to determine the unknowns. Some basic steps are applied to determine the unknown forces and moments. They are summarized below:
Draw the free-body diagram of the beam
The beam is isolated from the supports; depending upon the loading condition and the type of beam, a free-body diagram of the beam is drawn. In the free body diagram, all the external forces and the reaction forces are indicated. Drawing a free-body diagram is a way of simplifying the problem.
Check of determinacy
If the number of reactions is more than the available equilibrium equations, the beam is regarded as statically indeterminate. The beam unknowns cannot be solved using the three equilibrium equations alone. A compatibility equation is to be used because it considers the deformation equations of the beam to determine the unknowns. If the number of reactions of the beam is equal to the number of equilibrium equations, the beam unknowns can be easily solved using the available equilibrium equations.
Apply equilibrium equations
There are basically three equilibrium equations. They are: , , . Here, represents all the forces along the X direction, represents all the forces along the Y direction, and represents all the moments and torques experienced by the beam. A moment causes bending in the beam, while a torque causes a beam to undergo twisting.
Appropriate sign convention must be followed to analyze the beams.
Context and Applications
The topic is majorly taught in first-year engineering degree courses of civil engineering and mechanical engineering. The topic is also taught in other degree courses such as bachelor of science and master of science. Besides, the topic finds its extensive applications in the construction sector that requires designing and analysis of buildings and structures.
- Bachelors in Technology (Civil Engineering)
- Masters in Technology (Civil Engineering)
- Bachelors in Technology (Mechanical Engineering)
- Masters in Technology (Mechanical Engineering)
Practice Problems
1. Which of the following represents the correct number of equilibrium equations?
- Two
- Three
- Three including compatibility equations
- Two including compatibility equations
Correct option- b
Explanation: Three equilibrium equations are used to determine the unknown forces. If the beam is statically indeterminate, an additional equation called the compatibility equation is used.
2. Which of the following is true for the cantilever beam?
- It has one fixed end.
- It has two fixed ends.
- One of its ends is extended outside the supports.
- All of these
Correct option- a
Explanation: A cantilever beam is a beam that has one of its ends free and the other end fixed.
3. Which of the following is true for simply supported beams?
- It has one fixed support and a roller support
- It has both its ends fixed
- It has both its ends as fixed supports
- None of these
Correct option- a
Explanation: A simply supported beam is a beam whose one end remains fixed while the other end remains roller supported.
4. Which of the following is true for a beam?
- Beam supports shear loads
- Beam supports bending moments
- Beam supports axial loads
- All of these
Correct option- a
Explanation: A beam is a member that only supports shear loads
5. Which of the following represents the number of degrees of freedom for roller support?
- Two
- One
- Three
- Zero
Correct option- a
Explanation: The number of degrees of freedom for roller support is two.
Want more help with your civil engineering homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.
Strength of materials
Investigation of forces, force systems, loading and reactions
Loads and reactive forces
Loads and Reactive Forces Homework Questions from Fellow Students
Browse our recently answered Loads and Reactive Forces homework questions.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.